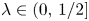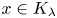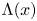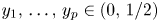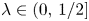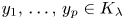Refine search
Actions for selected content:
28972 results in Differential and integral equations, dynamical systems and control theory
JMJ volume 23 issue 4 Cover and Back matter
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 4 / July 2024
- Published online by Cambridge University Press:
- 03 October 2024, pp. b1-b2
- Print publication:
- July 2024
-
- Article
-
- You have access
- Export citation
Rigidity for the perimeter inequality under Schwarz symmetrization
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 03 June 2024, pp. 1-27
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
TWISTED ACTIONS ON COHOMOLOGIES AND BIMODULES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 117 / Issue 2 / October 2024
- Published online by Cambridge University Press:
- 31 May 2024, pp. 187-238
- Print publication:
- October 2024
-
- Article
- Export citation
METHODOLOGY AND CHALLENGES OF SURROGATE MODELLING METHODS FOR MULTI-FIDELITY EXPENSIVE BLACK-BOX PROBLEMS
-
- Journal:
- The ANZIAM Journal / Volume 66 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 31 May 2024, pp. 35-61
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Indistinguishable asymptotic pairs and multidimensional Sturmian configurations
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 2 / February 2025
- Published online by Cambridge University Press:
- 31 May 2024, pp. 337-395
- Print publication:
- February 2025
-
- Article
- Export citation
EVALUATION FUNCTIONS AND REFLEXIVITY OF BANACH SPACES OF HOLOMORPHIC FUNCTIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 118 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 31 May 2024, pp. 164-177
- Print publication:
- April 2025
-
- Article
- Export citation
Preface
-
- Book:
- Groups and Graphs, Designs and Dynamics
- Published online:
- 11 May 2024
- Print publication:
- 30 May 2024, pp xiii-xvi
-
- Chapter
- Export citation
3 - Laplacian eigenvalues and optimality
-
-
- Book:
- Groups and Graphs, Designs and Dynamics
- Published online:
- 11 May 2024
- Print publication:
- 30 May 2024, pp 176-265
-
- Chapter
- Export citation
Contents
-
- Book:
- Groups and Graphs, Designs and Dynamics
- Published online:
- 11 May 2024
- Print publication:
- 30 May 2024, pp v-x
-
- Chapter
- Export citation
Frontmatter
-
- Book:
- Groups and Graphs, Designs and Dynamics
- Published online:
- 11 May 2024
- Print publication:
- 30 May 2024, pp i-iv
-
- Chapter
- Export citation
Author Index
-
- Book:
- Groups and Graphs, Designs and Dynamics
- Published online:
- 11 May 2024
- Print publication:
- 30 May 2024, pp 423-426
-
- Chapter
- Export citation
4 - Symbolic dynamics and the stable algebra of matrices
-
-
- Book:
- Groups and Graphs, Designs and Dynamics
- Published online:
- 11 May 2024
- Print publication:
- 30 May 2024, pp 266-422
-
- Chapter
- Export citation
Authors
-
- Book:
- Groups and Graphs, Designs and Dynamics
- Published online:
- 11 May 2024
- Print publication:
- 30 May 2024, pp xi-xii
-
- Chapter
- Export citation
2 - Quantum probability approach to spectral analysis of growing graphs
-
-
- Book:
- Groups and Graphs, Designs and Dynamics
- Published online:
- 11 May 2024
- Print publication:
- 30 May 2024, pp 87-175
-
- Chapter
- Export citation
Subject Index
-
- Book:
- Groups and Graphs, Designs and Dynamics
- Published online:
- 11 May 2024
- Print publication:
- 30 May 2024, pp 427-434
-
- Chapter
- Export citation
The homotopy decomposition of the suspension of a non-simply-connected five-manifold – ADDENDUM
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 30 May 2024, p. 1
-
- Article
- Export citation
On a class of self-similar sets which contain finitely many common points
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 30 May 2024, pp. 1-22
-
- Article
- Export citation
1 - Topics in representation theory of finite groups
-
-
- Book:
- Groups and Graphs, Designs and Dynamics
- Published online:
- 11 May 2024
- Print publication:
- 30 May 2024, pp 1-86
-
- Chapter
- Export citation
Maintenance of steady-state mRNA levels by a microRNA-based feed forward loop in the presence of stochastic gene expression noise
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 36 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 29 May 2024, pp. 143-160
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Uniform syndeticity in multiple recurrence
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 2 / February 2025
- Published online by Cambridge University Press:
- 28 May 2024, pp. 504-525
- Print publication:
- February 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation