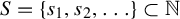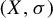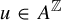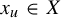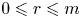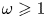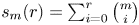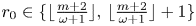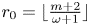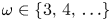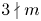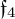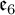Refine search
Actions for selected content:
28972 results in Differential and integral equations, dynamical systems and control theory
Deformational rigidity of integrable metrics on the torus
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 2 / February 2025
- Published online by Cambridge University Press:
- 09 September 2024, pp. 467-503
- Print publication:
- February 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Minimal zero entropy subshifts can be unrestricted along any sparse set
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 2 / February 2025
- Published online by Cambridge University Press:
- 09 September 2024, pp. 566-572
- Print publication:
- February 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ETS volume 44 issue 9 Cover and Front matter
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 9 / September 2024
- Published online by Cambridge University Press:
- 30 September 2024, pp. f1-f2
- Print publication:
- September 2024
-
- Article
-
- You have access
- Export citation
ETS volume 44 issue 9 Cover and Back matter
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 9 / September 2024
- Published online by Cambridge University Press:
- 30 September 2024, pp. b1-b2
- Print publication:
- September 2024
-
- Article
-
- You have access
- Export citation
JMJ volume 23 issue 5 Cover and Back matter
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 5 / September 2024
- Published online by Cambridge University Press:
- 08 November 2024, pp. b1-b2
- Print publication:
- September 2024
-
- Article
-
- You have access
- Export citation
JMJ volume 23 issue 5 Cover and Front matter
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 5 / September 2024
- Published online by Cambridge University Press:
- 08 November 2024, pp. f1-f2
- Print publication:
- September 2024
-
- Article
-
- You have access
- Export citation
GMJ volume 66 issue 3 Cover and Back matter
-
- Journal:
- Glasgow Mathematical Journal / Volume 66 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 22 November 2024, pp. b1-b2
- Print publication:
- September 2024
-
- Article
-
- You have access
- Export citation
GMJ volume 66 issue 3 Cover and Front matter
-
- Journal:
- Glasgow Mathematical Journal / Volume 66 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 22 November 2024, pp. f1-f2
- Print publication:
- September 2024
-
- Article
-
- You have access
- Export citation
Note on almost isometric ideals and local retracts in Banach and metric spaces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 27 August 2024, pp. 1-25
-
- Article
- Export citation
Maximizing weighted sums of binomial coefficients using generalized continued fractions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 27 August 2024, pp. 1-16
-
- Article
- Export citation
JAZ volume 117 issue 1 Cover and Back matter
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 117 / Issue 1 / August 2024
- Published online by Cambridge University Press:
- 30 September 2024, pp. b1-b2
- Print publication:
- August 2024
-
- Article
-
- You have access
- Export citation
PRM volume 154 issue 4 Cover and Back matter
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 4 / August 2024
- Published online by Cambridge University Press:
- 03 October 2024, pp. b1-b2
- Print publication:
- August 2024
-
- Article
-
- You have access
- Export citation
ETS volume 44 issue 8 Cover and Front matter
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 8 / August 2024
- Published online by Cambridge University Press:
- 23 September 2024, pp. f1-f2
- Print publication:
- August 2024
-
- Article
-
- You have access
- Export citation
ETS volume 44 issue 8 Cover and Back matter
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 8 / August 2024
- Published online by Cambridge University Press:
- 23 September 2024, pp. b1-b2
- Print publication:
- August 2024
-
- Article
-
- You have access
- Export citation
PRM volume 154 issue 4 Cover and Front matter
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 4 / August 2024
- Published online by Cambridge University Press:
- 03 October 2024, pp. f1-f2
- Print publication:
- August 2024
-
- Article
-
- You have access
- Export citation
JAZ volume 117 issue 1 Cover and Front matter
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 117 / Issue 1 / August 2024
- Published online by Cambridge University Press:
- 30 September 2024, pp. f1-f2
- Print publication:
- August 2024
-
- Article
-
- You have access
- Export citation
EXCEPTIONAL SIMPLE REAL LIE ALGEBRAS
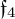 $\mathfrak {f}_4$ AND
$\mathfrak {f}_4$ AND 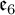 $\mathfrak {e}_6$ VIA CONTACTIFICATIONS
$\mathfrak {e}_6$ VIA CONTACTIFICATIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 03 July 2024, pp. 157-201
- Print publication:
- January 2025
-
- Article
- Export citation
JMJ volume 23 issue 4 Cover and Front matter
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 4 / July 2024
- Published online by Cambridge University Press:
- 03 October 2024, pp. f1-f2
- Print publication:
- July 2024
-
- Article
-
- You have access
- Export citation
ETS volume 44 issue 7 Cover and Front matter
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 7 / July 2024
- Published online by Cambridge University Press:
- 11 July 2024, pp. f1-f2
- Print publication:
- July 2024
-
- Article
-
- You have access
- Export citation
ETS volume 44 issue 7 Cover and Back matter
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 7 / July 2024
- Published online by Cambridge University Press:
- 11 July 2024, pp. b1-b2
- Print publication:
- July 2024
-
- Article
-
- You have access
- Export citation