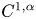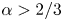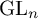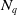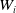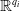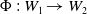Refine search
Actions for selected content:
28972 results in Differential and integral equations, dynamical systems and control theory
2 - Singularities in Action
-
- Book:
- Higher Special Functions
- Published online:
- 16 May 2024
- Print publication:
- 23 May 2024, pp 81-113
-
- Chapter
- Export citation
3 - Fuchsian Differential Equations: The Cornerstones
-
- Book:
- Higher Special Functions
- Published online:
- 16 May 2024
- Print publication:
- 23 May 2024, pp 114-156
-
- Chapter
- Export citation
Appendix A - Standard Central Two-Point Connection Problem
-
- Book:
- Higher Special Functions
- Published online:
- 16 May 2024
- Print publication:
- 23 May 2024, pp 281-292
-
- Chapter
- Export citation
On a localization-in-frequency approach for a class of elliptic problems with singular boundary data
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 21 May 2024, pp. 1-35
-
- Article
- Export citation
Opinion formation on evolving network: the DPA method applied to a nonlocal cross-diffusion PDE-ODE system
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 35 / Issue 6 / December 2024
- Published online by Cambridge University Press:
- 21 May 2024, pp. 748-775
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A global higher regularity result for the static relaxed micromorphic model on smooth domains
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 20 May 2024, pp. 1-15
-
- Article
- Export citation
The geometry of C1,α flat isometric immersions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 20 May 2024, pp. 1-39
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ARCHIMEDEAN NEWFORM THEORY FOR
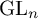 $\operatorname {\mathrm {GL}}_n$
$\operatorname {\mathrm {GL}}_n$
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 17 May 2024, pp. 41-116
- Print publication:
- January 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation

Higher Special Functions
- A Theory of the Central Two-Point Connection Problem Based on a Singularity Approach
-
- Published online:
- 16 May 2024
- Print publication:
- 23 May 2024
Diffuse-interface approximation and weak–strong uniqueness of anisotropic mean curvature flow
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 36 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 16 May 2024, pp. 82-142
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Stereographic compactification and affine bi-Lipschitz homeomorphisms
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 66 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 16 May 2024, pp. 582-596
- Print publication:
- September 2024
-
- Article
- Export citation
Binary pattern retrieval with Kuramoto-type oscillators via a least orthogonal lift of three patterns
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 36 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 16 May 2024, pp. 448-463
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
PRM volume 154 issue 3 Cover and Back matter
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 16 May 2024, pp. b1-b2
- Print publication:
- June 2024
-
- Article
-
- You have access
- Export citation
PRM volume 154 issue 3 Cover and Front matter
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 16 May 2024, pp. f1-f2
- Print publication:
- June 2024
-
- Article
-
- You have access
- Export citation
Homology and K-theory of dynamical systems IV. Further structural results on groupoid homology
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 15 May 2024, pp. 247-273
- Print publication:
- January 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Asymptotic profiles of a nonlocal dispersal SIS epidemic model with saturated incidence
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 14 May 2024, pp. 1-33
-
- Article
- Export citation
Flat model structures and Gorenstein objects in functor categories
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 14 May 2024, pp. 1-21
-
- Article
- Export citation
Sufficiency of
 $\boldsymbol{c}$-cyclical monotonicity in a class of multi-marginal optimal transport problems
$\boldsymbol{c}$-cyclical monotonicity in a class of multi-marginal optimal transport problems
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 36 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 14 May 2024, pp. 68-81
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Optimal decay for solutions of nonlocal semilinear equations with critical exponent in homogeneous groups
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 14 May 2024, pp. 1-29
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
JAZ volume 116 issue 3 Cover and Back matter
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 116 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 13 May 2024, pp. b1-b2
- Print publication:
- June 2024
-
- Article
-
- You have access
- Export citation