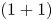Refine search
Actions for selected content:
28972 results in Differential and integral equations, dynamical systems and control theory
Spreading primitive groups of diagonal type do not exist
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 26 April 2024, pp. 1-11
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Poissonian pair correlation for directions in multi-dimensional affine lattices and escape of mass estimates for embedded horospheres
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 26 April 2024, pp. 218-246
- Print publication:
- January 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
WILES DEFECT OF HECKE ALGEBRAS VIA LOCAL-GLOBAL ARGUMENTS: WITH AN APPENDIX BY NAJMUDDIN FAKHRUDDIN AND CHANDRASHEKHAR B. KHARE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 6 / November 2024
- Published online by Cambridge University Press:
- 25 April 2024, pp. 2461-2541
- Print publication:
- November 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Bifurcation of the travelling wave solutions in a perturbed (1 + 1)-dimensional dispersive long wave equation via a geometric approach
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 25 April 2024, pp. 1-28
-
- Article
- Export citation
Modelling of the fluid flow in a thin domain with injection through permeable boundary
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 35 / Issue 6 / December 2024
- Published online by Cambridge University Press:
- 25 April 2024, pp. 776-796
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Khintchine-type double recurrence in abelian groups
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 24 April 2024, pp. 1-33
- Print publication:
- January 2025
-
- Article
- Export citation
Uniform propagation of chaos for a dollar exchange econophysics model
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 36 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 22 April 2024, pp. 27-39
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
EXPONENTIAL ASYMPTOTICS USING NUMERICAL RATIONAL APPROXIMATION IN LINEAR DIFFERENTIAL EQUATIONS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 65 / Issue 4 / October 2023
- Published online by Cambridge University Press:
- 22 April 2024, pp. 285-307
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Simplicial volume of manifolds with amenable fundamental group at infinity
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 66 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 22 April 2024, pp. 563-570
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
FLUID INJECTION IN A POROUS MEDIUM: THE RADIAL SAFFMAN–TAYLOR INSTABILITY
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 65 / Issue 4 / October 2023
- Published online by Cambridge University Press:
- 19 April 2024, pp. 347-383
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Singer conjecture for varieties with semismall Albanese map and residually finite fundamental group
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 19 April 2024, pp. 1-7
-
- Article
- Export citation
Macroscopic limit of a Fokker-Planck model of swarming rigid bodies
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 36 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 19 April 2024, pp. 349-397
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Schmidt games and Cantor winning sets
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 19 April 2024, pp. 71-110
- Print publication:
- January 2025
-
- Article
- Export citation
DETECTING MOISTURE IN BAUXITE USING MICROWAVES
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 65 / Issue 4 / October 2023
- Published online by Cambridge University Press:
- 17 April 2024, pp. 308-346
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE DISTINCTION OF IWAHORI-SPHERICAL DISCRETE SERIES REPRESENTATIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 17 April 2024, pp. 1-15
- Print publication:
- January 2025
-
- Article
- Export citation
The homotopy decomposition of the suspension of a non-simply-connected five-manifold
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 17 April 2024, pp. 1-29
-
- Article
- Export citation
Maximal subgroups of a family of iterated monodromy groups
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 66 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 17 April 2024, pp. 541-562
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Asymptotic distribution for pairs of linear and quadratic forms at integral vectors
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 17 April 2024, pp. 111-139
- Print publication:
- January 2025
-
- Article
- Export citation
KOBAYASHI-OCHIAI’S FINITENESS THEOREM FOR ORBIFOLD PAIRS OF GENERAL TYPE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 6 / November 2024
- Published online by Cambridge University Press:
- 17 April 2024, pp. 2713-2732
- Print publication:
- November 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Slow passage through the Busse balloon – predicting steps on the Eckhaus staircase
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 36 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 16 April 2024, pp. 1-26
-
- Article
-
- You have access
- Open access
- HTML
- Export citation