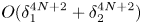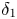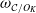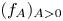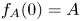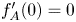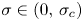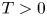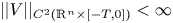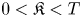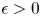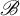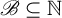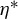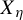Refine search
Actions for selected content:
28972 results in Differential and integral equations, dynamical systems and control theory
OPTIMAL QUEUING STRATEGIES FOR AN M/G/1 RETRIAL QUEUE SYSTEM WITH RWV AND ISEV POLICIES
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 65 / Issue 4 / October 2023
- Published online by Cambridge University Press:
- 19 March 2024, pp. 384-410
-
- Article
- Export citation
BASIC NONARCHIMEDEAN JØRGENSEN THEORY
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 117 / Issue 3 / December 2024
- Published online by Cambridge University Press:
- 19 March 2024, pp. 273-287
- Print publication:
- December 2024
-
- Article
- Export citation
Global index of real polynomials
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 18 March 2024, pp. 1-29
-
- Article
- Export citation
A mathematical analysis of the Kakinuma model for interfacial gravity waves. Part II: justification as a shallow water approximation
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 18 March 2024, pp. 1-72
-
- Article
- Export citation
Models and integral differentials of hyperelliptic curves
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 66 / Issue 2 / May 2024
- Published online by Cambridge University Press:
- 18 March 2024, pp. 382-439
- Print publication:
- May 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Rigidity of pressures of Hölder potentials and the fitting of analytic functions through them
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 12 / December 2024
- Published online by Cambridge University Press:
- 18 March 2024, pp. 3530-3564
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Approximate homomorphisms and sofic approximations of orbit equivalence relations
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 12 / December 2024
- Published online by Cambridge University Press:
- 15 March 2024, pp. 3455-3480
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THERMODYNAMIC FORMALISM FOR AMENABLE GROUPS AND COUNTABLE STATE SPACES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 6 / November 2024
- Published online by Cambridge University Press:
- 15 March 2024, pp. 2647-2711
- Print publication:
- November 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Eternal solutions to a porous medium equation with strong non-homogeneous absorption. Part I: radially non-increasing profiles
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 14 March 2024, pp. 1-22
-
- Article
- Export citation
Decay at infinity for solutions to some fractional parabolic equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 14 March 2024, pp. 1-37
-
- Article
- Export citation
ANZ VOLUME 65 ISSUE 3 COVER AND FRONT MATTER
-
- Journal:
- The ANZIAM Journal / Volume 65 / Issue 3 / July 2023
- Published online by Cambridge University Press:
- 12 March 2024, pp. f1-f2
-
- Article
-
- You have access
- Export citation
ANZ VOLUME 65 ISSUE 3 COVER AND BACK MATTER
-
- Journal:
- The ANZIAM Journal / Volume 65 / Issue 3 / July 2023
- Published online by Cambridge University Press:
- 12 March 2024, pp. b1-b6
-
- Article
-
- You have access
- Export citation
Examples of hyperbolic spaces without the properties of quasi-ball or bounded eccentricity
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 66 / Issue 2 / May 2024
- Published online by Cambridge University Press:
- 11 March 2024, pp. 440-448
- Print publication:
- May 2024
-
- Article
- Export citation
Measure transfer and S-adic developments for subshifts
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 11 / November 2024
- Published online by Cambridge University Press:
- 11 March 2024, pp. 3120-3154
- Print publication:
- November 2024
-
- Article
- Export citation
Necessary and sufficient conditions for ground state solutions to planar Kirchhoff-type equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 5 / October 2025
- Published online by Cambridge University Press:
- 11 March 2024, pp. 1938-1959
- Print publication:
- October 2025
-
- Article
- Export citation
JAZ volume 116 issue 2 Cover and Back matter
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 116 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 11 March 2024, pp. b1-b2
- Print publication:
- April 2024
-
- Article
-
- You have access
- Export citation
JAZ volume 116 issue 2 Cover and Front matter
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 116 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 11 March 2024, pp. f1-f2
- Print publication:
- April 2024
-
- Article
-
- You have access
- Export citation
FINITENESS OF CANONICAL QUOTIENTS OF DEHN QUANDLES OF SURFACES
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 118 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 11 March 2024, pp. 317-334
- Print publication:
- June 2025
-
- Article
- Export citation
Invariant measures for
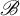 $\mathscr {B}$-free systems revisited
$\mathscr {B}$-free systems revisited
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 10 / October 2024
- Published online by Cambridge University Press:
- 08 March 2024, pp. 2901-2932
- Print publication:
- October 2024
-
- Article
- Export citation
Optimal inverse problems of potentials for two given eigenvalues of Sturm–Liouville problems
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 5 / October 2025
- Published online by Cambridge University Press:
- 07 March 2024, pp. 1914-1937
- Print publication:
- October 2025
-
- Article
- Export citation