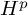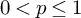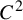Refine search
Actions for selected content:
28972 results in Differential and integral equations, dynamical systems and control theory
TRILINEAR FOURIER MULTIPLIERS ON HARDY SPACES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 5 / September 2024
- Published online by Cambridge University Press:
- 15 February 2024, pp. 2217-2278
- Print publication:
- September 2024
-
- Article
- Export citation
Stable laws for random dynamical systems
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 11 / November 2024
- Published online by Cambridge University Press:
- 14 February 2024, pp. 3041-3090
- Print publication:
- November 2024
-
- Article
- Export citation
On a self-embedding problem for self-similar sets
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 10 / October 2024
- Published online by Cambridge University Press:
- 14 February 2024, pp. 3002-3011
- Print publication:
- October 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The turnpike property for mean-field optimal control problems
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 35 / Issue 6 / December 2024
- Published online by Cambridge University Press:
- 12 February 2024, pp. 733-747
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the Sobolev stability threshold for shear flows near Couette in 2D MHD equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 5 / October 2025
- Published online by Cambridge University Press:
- 12 February 2024, pp. 1580-1630
- Print publication:
- October 2025
-
- Article
- Export citation
Dimension estimates and approximation in non-uniformly hyperbolic systems
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 10 / October 2024
- Published online by Cambridge University Press:
- 12 February 2024, pp. 2975-3001
- Print publication:
- October 2024
-
- Article
- Export citation
On the Γ-convergence of the Allen–Cahn functional with boundary conditions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 5 / October 2025
- Published online by Cambridge University Press:
- 12 February 2024, pp. 1557-1579
- Print publication:
- October 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
9 - Survey on Entropy-Type Invariants of Subexponential Growth in Dynamical Systems
-
- Book:
- A Vision for Dynamics in the 21st Century
- Published online:
- 01 February 2024
- Print publication:
- 08 February 2024, pp 232-289
-
- Chapter
- Export citation
2 - Rigidity of Topological Entropy of Boundary Maps Associated to Fuchsian Groups
-
- Book:
- A Vision for Dynamics in the 21st Century
- Published online:
- 01 February 2024
- Print publication:
- 08 February 2024, pp 19-47
-
- Chapter
- Export citation
5 - SRB and Equilibrium Measures via Dimension Theory
-
- Book:
- A Vision for Dynamics in the 21st Century
- Published online:
- 01 February 2024
- Print publication:
- 08 February 2024, pp 94-138
-
- Chapter
- Export citation
Frontmatter
-
- Book:
- A Vision for Dynamics in the 21st Century
- Published online:
- 01 February 2024
- Print publication:
- 08 February 2024, pp i-iv
-
- Chapter
- Export citation
1 - Open Problems from 2020 Vision for Dynamics Conference in Będlewo
-
- Book:
- A Vision for Dynamics in the 21st Century
- Published online:
- 01 February 2024
- Print publication:
- 08 February 2024, pp 1-18
-
- Chapter
- Export citation
10 - On the Smooth Realization Problem and the AbC Method
-
- Book:
- A Vision for Dynamics in the 21st Century
- Published online:
- 01 February 2024
- Print publication:
- 08 February 2024, pp 290-317
-
- Chapter
- Export citation
8 - Non-stationary Normal Forms for Contracting Extensions
-
- Book:
- A Vision for Dynamics in the 21st Century
- Published online:
- 01 February 2024
- Print publication:
- 08 February 2024, pp 207-231
-
- Chapter
- Export citation
6 - Abelian Livshits Theorems and Geometric Applications
-
- Book:
- A Vision for Dynamics in the 21st Century
- Published online:
- 01 February 2024
- Print publication:
- 08 February 2024, pp 139-167
-
- Chapter
- Export citation
4 - Recent Results and Open Questions on Pseudo-Rotations
-
- Book:
- A Vision for Dynamics in the 21st Century
- Published online:
- 01 February 2024
- Print publication:
- 08 February 2024, pp 67-93
-
- Chapter
- Export citation
Contents
-
- Book:
- A Vision for Dynamics in the 21st Century
- Published online:
- 01 February 2024
- Print publication:
- 08 February 2024, pp v-vi
-
- Chapter
- Export citation
3 - Flexibility of Entropies for Piecewise Expanding Unimodal Maps
-
- Book:
- A Vision for Dynamics in the 21st Century
- Published online:
- 01 February 2024
- Print publication:
- 08 February 2024, pp 48-66
-
- Chapter
- Export citation
11 - On Some Spectral Problems in Ergodic Theory
-
- Book:
- A Vision for Dynamics in the 21st Century
- Published online:
- 01 February 2024
- Print publication:
- 08 February 2024, pp 318-336
-
- Chapter
- Export citation
13 - Linear Cocycles over Hyperbolic Systems
-
- Book:
- A Vision for Dynamics in the 21st Century
- Published online:
- 01 February 2024
- Print publication:
- 08 February 2024, pp 384-434
-
- Chapter
- Export citation