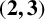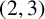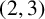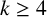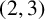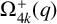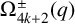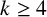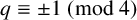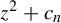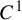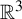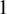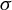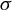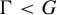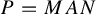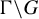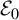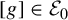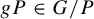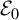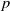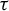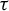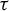Refine search
Actions for selected content:
28972 results in Differential and integral equations, dynamical systems and control theory
THE
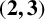 $\boldsymbol {(2,3)}$-GENERATION OF THE FINITE SIMPLE ODD-DIMENSIONAL ORTHOGONAL GROUPS
$\boldsymbol {(2,3)}$-GENERATION OF THE FINITE SIMPLE ODD-DIMENSIONAL ORTHOGONAL GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 117 / Issue 2 / October 2024
- Published online by Cambridge University Press:
- 28 February 2024, pp. 130-148
- Print publication:
- October 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Derivation and travelling wave analysis of phenotype-structured haptotaxis models of cancer invasion
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 36 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 27 February 2024, pp. 231-263
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Multiplicity of positive solutions for a class of nonhomogeneous elliptic equations in the hyperbolic space
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 5 / October 2025
- Published online by Cambridge University Press:
- 27 February 2024, pp. 1708-1746
- Print publication:
- October 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the stochastic bifurcations regarding random iterations of polynomials of the form
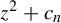 $z^{2} + c_{n}$
$z^{2} + c_{n}$
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 11 / November 2024
- Published online by Cambridge University Press:
- 26 February 2024, pp. 3358-3384
- Print publication:
- November 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A collision result for both non-Newtonian and heat conducting Newtonian compressible fluids
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 5 / October 2025
- Published online by Cambridge University Press:
- 26 February 2024, pp. 1631-1645
- Print publication:
- October 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Qualitative properties of solutions for system involving the fractional Laplacian
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 5 / October 2025
- Published online by Cambridge University Press:
- 26 February 2024, pp. 1661-1676
- Print publication:
- October 2025
-
- Article
- Export citation
Common valuations of division polynomials
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 5 / October 2025
- Published online by Cambridge University Press:
- 26 February 2024, pp. 1646-1660
- Print publication:
- October 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Nonlocal anisotropic interactions of Coulomb type
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 5 / October 2025
- Published online by Cambridge University Press:
- 26 February 2024, pp. 1677-1707
- Print publication:
- October 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Shifts of finite type on locally finite groups
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 12 / December 2024
- Published online by Cambridge University Press:
- 26 February 2024, pp. 3565-3598
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ACTIVE REMODELLING OF TISSUES TO DESCRIBE BIPHASIC RHEOLOGICAL RESPONSES
-
- Journal:
- The ANZIAM Journal / Volume 65 / Issue 3 / July 2023
- Published online by Cambridge University Press:
- 26 February 2024, pp. 195-214
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Upper, down, two-sided Lorenz attractor, collisions, merging, and switching
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 10 / October 2024
- Published online by Cambridge University Press:
- 21 February 2024, pp. 2737-2781
- Print publication:
- October 2024
-
- Article
- Export citation
A data-driven kinetic model for opinion dynamics with social network contacts
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 36 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 20 February 2024, pp. 264-290
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Measures of maximal entropy of bounded density shifts
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 10 / October 2024
- Published online by Cambridge University Press:
- 20 February 2024, pp. 2960-2974
- Print publication:
- October 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On denseness of horospheres in higher rank homogeneous spaces
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 11 / November 2024
- Published online by Cambridge University Press:
- 19 February 2024, pp. 3272-3289
- Print publication:
- November 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
PERFECTING GROUP SCHEMES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 6 / November 2024
- Published online by Cambridge University Press:
- 16 February 2024, pp. 2549-2591
- Print publication:
- November 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On twisted group ring isomorphism problem for p-groups
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 66 / Issue 2 / May 2024
- Published online by Cambridge University Press:
- 16 February 2024, pp. 368-381
- Print publication:
- May 2024
-
- Article
- Export citation
LIMIT SETS OF UNFOLDING PATHS IN OUTER SPACE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 5 / September 2024
- Published online by Cambridge University Press:
- 15 February 2024, pp. 2365-2403
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE ITERATIONS AND THE ARGUMENT DISTRIBUTION OF MEROMORPHIC FUNCTIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 116 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 15 February 2024, pp. 145-170
- Print publication:
- April 2024
-
- Article
- Export citation
Invariant sets and nilpotency of endomorphisms of algebraic sofic shifts
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 10 / October 2024
- Published online by Cambridge University Press:
- 15 February 2024, pp. 2859-2900
- Print publication:
- October 2024
-
- Article
- Export citation
Sufficient conditions for non-zero entropy of closed relations
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 11 / November 2024
- Published online by Cambridge University Press:
- 15 February 2024, pp. 3091-3119
- Print publication:
- November 2024
-
- Article
- Export citation