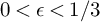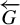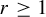Refine search
Actions for selected content:
28972 results in Differential and integral equations, dynamical systems and control theory
AN EFFECTIVE UPPER BOUND FOR ANTI-CANONICAL VOLUMES OF SINGULAR FANO THREEFOLDS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 6 / November 2024
- Published online by Cambridge University Press:
- 07 March 2024, pp. 2631-2646
- Print publication:
- November 2024
-
- Article
- Export citation
Index estimates of compact hypersurfaces in smooth metric measure spaces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 5 / October 2025
- Published online by Cambridge University Press:
- 07 March 2024, pp. 1895-1913
- Print publication:
- October 2025
-
- Article
- Export citation
Non-integrability of the restricted three-body problem
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 10 / October 2024
- Published online by Cambridge University Press:
- 06 March 2024, pp. 3012-3040
- Print publication:
- October 2024
-
- Article
- Export citation
RADU GROUPS ACTING ON TREES ARE CCR
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 117 / Issue 2 / October 2024
- Published online by Cambridge University Press:
- 06 March 2024, pp. 149-186
- Print publication:
- October 2024
-
- Article
- Export citation
Bohr chaoticity of principal algebraic actions and Riesz product measures
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 10 / October 2024
- Published online by Cambridge University Press:
- 06 March 2024, pp. 2933-2959
- Print publication:
- October 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Tracial weights on topological graph algebras
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 12 / December 2024
- Published online by Cambridge University Press:
- 05 March 2024, pp. 3428-3454
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
An embedding theorem for subshifts over amenable groups with the comparison property
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 11 / November 2024
- Published online by Cambridge University Press:
- 05 March 2024, pp. 3155-3185
- Print publication:
- November 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ETS volume 44 issue 4 Cover and Back matter
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 4 / April 2024
- Published online by Cambridge University Press:
- 05 March 2024, pp. b1-b2
- Print publication:
- April 2024
-
- Article
-
- You have access
- Export citation
ETS volume 44 issue 4 Cover and Front matter
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 4 / April 2024
- Published online by Cambridge University Press:
- 05 March 2024, pp. f1-f2
- Print publication:
- April 2024
-
- Article
-
- You have access
- Export citation
PRM volume 154 issue 2 Cover and Back matter
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 05 March 2024, pp. b1-b2
- Print publication:
- April 2024
-
- Article
-
- You have access
- Export citation
PRM volume 154 issue 2 Cover and Front matter
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 05 March 2024, pp. f1-f2
- Print publication:
- April 2024
-
- Article
-
- You have access
- Export citation
Patterson–Sullivan theory for groups with a strongly contracting element
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 11 / November 2024
- Published online by Cambridge University Press:
- 05 March 2024, pp. 3216-3271
- Print publication:
- November 2024
-
- Article
- Export citation
Invariant measures and large deviation principles for stochastic Schrödinger delay lattice systems
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 5 / October 2025
- Published online by Cambridge University Press:
- 04 March 2024, pp. 1813-1854
- Print publication:
- October 2025
-
- Article
- Export citation
Bifurcations and pattern formation in a host–parasitoid model with nonlocal effect
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 5 / October 2025
- Published online by Cambridge University Press:
- 04 March 2024, pp. 1855-1894
- Print publication:
- October 2025
-
- Article
- Export citation
ENERGY BOUNDS FOR MODULAR ROOTS AND THEIR APPLICATIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 5 / September 2025
- Published online by Cambridge University Press:
- 04 March 2024, pp. 1765-1806
- Print publication:
- September 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Invariant measures of Toeplitz subshifts on non-amenable groups
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 11 / November 2024
- Published online by Cambridge University Press:
- 04 March 2024, pp. 3186-3215
- Print publication:
- November 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
JMJ volume 23 issue 2 Cover and Back matter
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 2 / March 2024
- Published online by Cambridge University Press:
- 19 March 2024, pp. b1-b2
- Print publication:
- March 2024
-
- Article
-
- You have access
- Export citation
JMJ volume 23 issue 2 Cover and Front matter
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 2 / March 2024
- Published online by Cambridge University Press:
- 19 March 2024, pp. f1-f2
- Print publication:
- March 2024
-
- Article
-
- You have access
- Export citation
On a critical time-harmonic Maxwell equation in nonlocal media
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 5 / October 2025
- Published online by Cambridge University Press:
- 29 February 2024, pp. 1747-1791
- Print publication:
- October 2025
-
- Article
- Export citation
Invariant set generated by a nonreal number is everywhere dense
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 5 / October 2025
- Published online by Cambridge University Press:
- 29 February 2024, pp. 1792-1812
- Print publication:
- October 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation