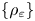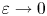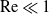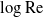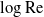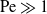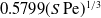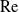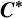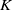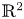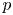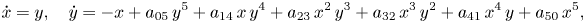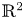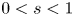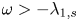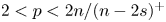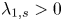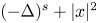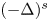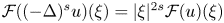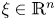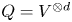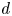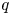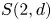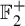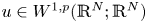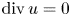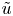Refine search
Actions for selected content:
28972 results in Differential and integral equations, dynamical systems and control theory
Sharp conditions for the validity of the Bourgain–Brezis–Mironescu formula
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 16 April 2024, pp. 1-24
-
- Article
- Export citation
A finite-volume scheme for fractional diffusion on bounded domains
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 36 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 16 April 2024, pp. 398-418
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Large Péclet number forced convection from a circular wire in a uniform stream: hybrid approximations at small Reynolds numbers
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 35 / Issue 6 / December 2024
- Published online by Cambridge University Press:
- 16 April 2024, pp. 823-834
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Linear actions of $\mathbb {Z}/p\times \mathbb {Z}/p$
 on $S^{2n-1}\times S^{2n-1}$
on $S^{2n-1}\times S^{2n-1}$
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 6 / December 2024
- Published online by Cambridge University Press:
- 16 April 2024, pp. 1699-1712
- Print publication:
- December 2024
-
- Article
- Export citation
SPHERICAL REPRESENTATIONS FOR
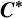 $\boldsymbol C^{\boldsymbol {*}}$-FLOWS III: WEIGHT-EXTENDED BRANCHING GRAPHS
$\boldsymbol C^{\boldsymbol {*}}$-FLOWS III: WEIGHT-EXTENDED BRANCHING GRAPHS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 117 / Issue 2 / October 2024
- Published online by Cambridge University Press:
- 15 April 2024, pp. 239-272
- Print publication:
- October 2024
-
- Article
- Export citation
Similarities and differences between specification and non-uniform specification
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 12 / December 2024
- Published online by Cambridge University Press:
- 15 April 2024, pp. 3501-3529
- Print publication:
- December 2024
-
- Article
- Export citation
Twisted Blanchfield pairings and twisted signatures III: Applications
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 66 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 15 April 2024, pp. 501-540
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A note on quantum K-theory of root constructions
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 66 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 12 April 2024, pp. 494-500
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Non-existence of a universal zero-entropy system via generic actions of almost complete growth
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 12 / December 2024
- Published online by Cambridge University Press:
- 12 April 2024, pp. 3630-3644
- Print publication:
- December 2024
-
- Article
- Export citation
On the Hausdorff dimension of invariant measures of piecewise smooth circle homeomorphisms
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 12 / December 2024
- Published online by Cambridge University Press:
- 11 April 2024, pp. 3599-3629
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Global centres in a class of quintic polynomial differential systems
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 11 April 2024, pp. 1-16
-
- Article
- Export citation
Uniqueness of ground states to fractional nonlinear elliptic equations with harmonic potential
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 11 April 2024, pp. 1-14
-
- Article
- Export citation
GENERALISED QUADRATIC FORMS OVER TOTALLY REAL NUMBER FIELDS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 6 / November 2024
- Published online by Cambridge University Press:
- 11 April 2024, pp. 2859-2912
- Print publication:
- November 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Quasi-hereditary covers of Temperley–Lieb algebras and relative dominant dimension
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 11 April 2024, pp. 1-38
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On almost quotient Yamabe solitons
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 66 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 11 April 2024, pp. 479-493
- Print publication:
- September 2024
-
- Article
- Export citation
Galois points and Cremona transformations
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 66 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 11 April 2024, pp. 471-478
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Substreetutions and more on trees
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 9 / September 2024
- Published online by Cambridge University Press:
- 08 April 2024, pp. 2399-2453
- Print publication:
- September 2024
-
- Article
- Export citation
Consensus-based optimisation with truncated noise
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 36 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 05 April 2024, pp. 292-315
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Unconditional convergence of eigenfunction expansions for abstract and elliptic operators
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 05 April 2024, pp. 1-19
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
An alternative approach to solenoidal Lipschitz truncation
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 05 April 2024, pp. 1-25
-
- Article
-
- You have access
- Open access
- HTML
- Export citation