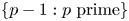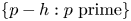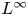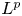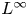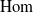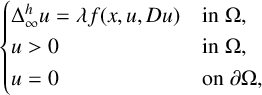Refine search
Actions for selected content:
28972 results in Differential and integral equations, dynamical systems and control theory
Structural stability of transonic shock flows with an external force
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 05 April 2024, pp. 1-24
-
- Article
- Export citation
Density of mode-locking property for quasi-periodically forced Arnold circle maps
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 12 / December 2024
- Published online by Cambridge University Press:
- 04 April 2024, pp. 3645-3680
- Print publication:
- December 2024
-
- Article
- Export citation
ETS volume 44 issue 5 Cover and Back matter
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 5 / May 2024
- Published online by Cambridge University Press:
- 04 April 2024, pp. b1-b2
- Print publication:
- May 2024
-
- Article
-
- You have access
- Export citation
ETS volume 44 issue 5 Cover and Front matter
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 5 / May 2024
- Published online by Cambridge University Press:
- 04 April 2024, pp. f1-f2
- Print publication:
- May 2024
-
- Article
-
- You have access
- Export citation
A data-driven kinetic model for opinion dynamics with social network contacts – ADDENDUM
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 36 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 02 April 2024, p. 291
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE p-ADIC GROSS–ZAGIER FORMULA ON SHIMURA CURVES, II: NONSPLIT PRIMES – CORRIGENDUM
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 6 / November 2024
- Published online by Cambridge University Press:
- 02 April 2024, pp. 2543-2548
- Print publication:
- November 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Entropy, virtual Abelianness and Shannon orbit equivalence
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 12 / December 2024
- Published online by Cambridge University Press:
- 02 April 2024, pp. 3481-3500
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Unit fractions with shifted prime denominators
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 02 April 2024, pp. 1-11
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
DYNAMICAL MCDUFF-TYPE PROPERTIES FOR GROUP ACTIONS ON VON NEUMANN ALGEBRAS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 6 / November 2024
- Published online by Cambridge University Press:
- 02 April 2024, pp. 2593-2629
- Print publication:
- November 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A NONCOMMUTATIVE ANALOGUE OF CLAUSEN’S VIEW ON THE IDÈLE CLASS GROUP
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 6 / November 2024
- Published online by Cambridge University Press:
- 02 April 2024, pp. 2777-2824
- Print publication:
- November 2024
-
- Article
- Export citation
Skew group categories, algebras associated to Cartan matrices and folding of root lattices
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 01 April 2024, pp. 1-45
-
- Article
- Export citation
On the reconstruction of unknown driving forces from low-mode observations in the 2D Navier–Stokes equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 01 April 2024, pp. 1-24
-
- Article
- Export citation
Torsion in classifying spaces of gauge groups
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 01 April 2024, pp. 1-16
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Tropical graph curves
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 01 April 2024, pp. 1-29
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Generalized second order vectorial ∞-eigenvalue problems
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 27 March 2024, pp. 1-21
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Measuring multidimensional heterogeneity in emergent social phenomena
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 36 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 25 March 2024, pp. 316-327
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Scale recurrence lemma and dimension formula for Cantor sets in the complex plane
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 11 / November 2024
- Published online by Cambridge University Press:
- 25 March 2024, pp. 3316-3357
- Print publication:
- November 2024
-
- Article
- Export citation
Triangular matrix categories over quasi-hereditary categories
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 66 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 21 March 2024, pp. 449-470
- Print publication:
- September 2024
-
- Article
- Export citation
Limit cycles in a rotated family of generalized Liénard systems allowing for finitely many switching lines
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 21 March 2024, pp. 1-29
-
- Article
- Export citation
VISCOSITY SOLUTIONS TO THE INFINITY LAPLACIAN EQUATION WITH SINGULAR NONLINEAR TERMS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 117 / Issue 3 / December 2024
- Published online by Cambridge University Press:
- 20 March 2024, pp. 345-374
- Print publication:
- December 2024
-
- Article
- Export citation