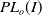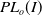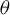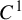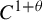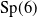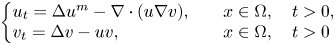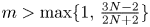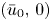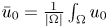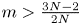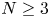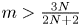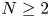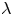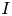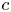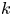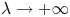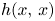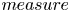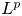Refine search
Actions for selected content:
28972 results in Differential and integral equations, dynamical systems and control theory
Some recent developments in Arnold diffusion
-
-
- Book:
- Hamiltonian Systems
- Published online:
- 10 May 2024
- Print publication:
- 09 May 2024, pp 75-110
-
- Chapter
- Export citation
Unified framework for the separation property in binary phase-segregation processes with singular entropy densities
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 36 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 09 May 2024, pp. 40-67
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A symplectic approach to Arnold diffusion problems
-
-
- Book:
- Hamiltonian Systems
- Published online:
- 10 May 2024
- Print publication:
- 09 May 2024, pp 229-296
-
- Chapter
- Export citation
Girth Alternative for subgroups of
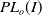 $PL_o(I)$
$PL_o(I)$
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 67 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 09 May 2024, pp. 1-10
- Print publication:
- January 2025
-
- Article
- Export citation
On invariant holonomies between centers
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 08 May 2024, pp. 274-293
- Print publication:
- January 2025
-
- Article
- Export citation
Weighted topological pressure revisited
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 08 May 2024, pp. 34-70
- Print publication:
- January 2025
-
- Article
- Export citation
ETS volume 44 issue 6 Cover and Back matter
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 6 / June 2024
- Published online by Cambridge University Press:
- 06 May 2024, pp. b1-b2
- Print publication:
- June 2024
-
- Article
-
- You have access
- Export citation
ETS volume 44 issue 6 Cover and Front matter
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 6 / June 2024
- Published online by Cambridge University Press:
- 06 May 2024, pp. f1-f2
- Print publication:
- June 2024
-
- Article
-
- You have access
- Export citation
Thinness of some hypergeometric groups in
 $\mathrm{Sp}(6)$
$\mathrm{Sp}(6)$
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 66 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 02 May 2024, pp. 571-581
- Print publication:
- September 2024
-
- Article
- Export citation
Threshold dynamics scenario of a plants-pollinators cooperative system with impulsive effect on a periodically evolving domain
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 35 / Issue 6 / December 2024
- Published online by Cambridge University Press:
- 02 May 2024, pp. 797-822
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
JMJ volume 23 issue 3 Cover and Front matter
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 3 / May 2024
- Published online by Cambridge University Press:
- 08 May 2024, pp. f1-f2
- Print publication:
- May 2024
-
- Article
-
- You have access
- Export citation
ADDENDUM: REAL TOPOLOGICAL HOCHSCHILD HOMOLOGY OF SCHEMES
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 3 / May 2024
- Published online by Cambridge University Press:
- 08 May 2024, pp. 1519-1520
- Print publication:
- May 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
JMJ volume 23 issue 3 Cover and Back matter
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 3 / May 2024
- Published online by Cambridge University Press:
- 08 May 2024, pp. b1-b2
- Print publication:
- May 2024
-
- Article
-
- You have access
- Export citation
GMJ volume 66 issue 2 Cover and Back matter
-
- Journal:
- Glasgow Mathematical Journal / Volume 66 / Issue 2 / May 2024
- Published online by Cambridge University Press:
- 05 November 2024, pp. b1-b2
- Print publication:
- May 2024
-
- Article
-
- You have access
- Export citation
GMJ volume 66 issue 2 Cover and Front matter
-
- Journal:
- Glasgow Mathematical Journal / Volume 66 / Issue 2 / May 2024
- Published online by Cambridge University Press:
- 05 November 2024, pp. f1-f2
- Print publication:
- May 2024
-
- Article
-
- You have access
- Export citation
Emergent behaviours of a non-abelian quantum synchronisation model over the unitary group
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 36 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 30 April 2024, pp. 328-348
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Flocking dynamics of agents moving with a constant speed and a randomly switching topology
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 36 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 30 April 2024, pp. 419-447
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Global boundedness and large time behaviour in a higher-dimensional quasilinear chemotaxis system with consumption of chemoattractant
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 30 April 2024, pp. 1-26
-
- Article
- Export citation
Desingularization of 2D elliptic free-boundary problem with non-autonomous nonlinearity
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 30 April 2024, pp. 1-38
-
- Article
- Export citation
Topologically free actions and ideals in twisted Banach algebra crossed products
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 26 April 2024, pp. 1-31
-
- Article
- Export citation