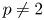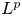Refine search
Actions for selected content:
28981 results in Differential and integral equations, dynamical systems and control theory
4 - Symbolic dynamics and the stable algebra of matrices
-
-
- Book:
- Groups and Graphs, Designs and Dynamics
- Published online:
- 11 May 2024
- Print publication:
- 30 May 2024, pp 266-422
-
- Chapter
- Export citation
Authors
-
- Book:
- Groups and Graphs, Designs and Dynamics
- Published online:
- 11 May 2024
- Print publication:
- 30 May 2024, pp xi-xii
-
- Chapter
- Export citation
2 - Quantum probability approach to spectral analysis of growing graphs
-
-
- Book:
- Groups and Graphs, Designs and Dynamics
- Published online:
- 11 May 2024
- Print publication:
- 30 May 2024, pp 87-175
-
- Chapter
- Export citation
Subject Index
-
- Book:
- Groups and Graphs, Designs and Dynamics
- Published online:
- 11 May 2024
- Print publication:
- 30 May 2024, pp 427-434
-
- Chapter
- Export citation
The homotopy decomposition of the suspension of a non-simply-connected five-manifold – ADDENDUM
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 30 May 2024, p. 1
-
- Article
- Export citation
On a class of self-similar sets which contain finitely many common points
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 30 May 2024, pp. 1-22
-
- Article
- Export citation
1 - Topics in representation theory of finite groups
-
-
- Book:
- Groups and Graphs, Designs and Dynamics
- Published online:
- 11 May 2024
- Print publication:
- 30 May 2024, pp 1-86
-
- Chapter
- Export citation
Maintenance of steady-state mRNA levels by a microRNA-based feed forward loop in the presence of stochastic gene expression noise
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 36 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 29 May 2024, pp. 143-160
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Uniform syndeticity in multiple recurrence
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 2 / February 2025
- Published online by Cambridge University Press:
- 28 May 2024, pp. 504-525
- Print publication:
- February 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Lp positivity preservation and self-adjointness of Schrödinger operators on incomplete Riemannian manifolds
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 28 May 2024, pp. 1-19
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Distribution in homology classes and discrete fractal dimension
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 28 May 2024, pp. 1-8
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
COHOMOLOGIE DE DE RHAM DU REVÊTEMENT MODÉRÉ DE L’ESPACE DE DRINFELD
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 6 / November 2024
- Published online by Cambridge University Press:
- 28 May 2024, pp. 2733-2775
- Print publication:
- November 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Partially hyperbolic endomorphisms with expanding linear part
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 2 / February 2025
- Published online by Cambridge University Press:
- 28 May 2024, pp. 321-336
- Print publication:
- February 2025
-
- Article
- Export citation
Spectral asymptotics for linear elasticity: the case of mixed boundary conditions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 24 May 2024, pp. 1-30
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ELECTRO-OSMOTIC EFFECT ON PERISTALTIC FLOW OF PHAN–THIEN–TANNER FLUID IN A PLANAR CHANNEL
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 66 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 24 May 2024, pp. 77-97
-
- Article
- Export citation
TWISTED GAN–GROSS–PRASAD CONJECTURE FOR CERTAIN TEMPERED L-PACKETS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 24 May 2024, pp. 17-39
- Print publication:
- January 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
References
-
- Book:
- Higher Special Functions
- Published online:
- 16 May 2024
- Print publication:
- 23 May 2024, pp 296-297
-
- Chapter
- Export citation
Appendix B - Curriculum Vitae of George Cecil Jaffé
-
- Book:
- Higher Special Functions
- Published online:
- 16 May 2024
- Print publication:
- 23 May 2024, pp 293-295
-
- Chapter
- Export citation
Frontmatter
-
- Book:
- Higher Special Functions
- Published online:
- 16 May 2024
- Print publication:
- 23 May 2024, pp i-iv
-
- Chapter
- Export citation
Contents
-
- Book:
- Higher Special Functions
- Published online:
- 16 May 2024
- Print publication:
- 23 May 2024, pp vii-viii
-
- Chapter
- Export citation