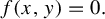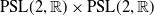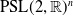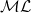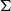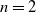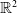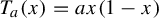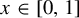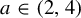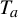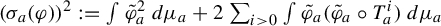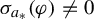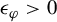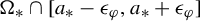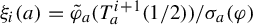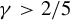Refine search
Actions for selected content:
28972 results in Differential and integral equations, dynamical systems and control theory
ETS volume 44 issue 11 Cover and Back matter
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 11 / November 2024
- Published online by Cambridge University Press:
- 03 October 2024, pp. b1-b2
- Print publication:
- November 2024
-
- Article
-
- You have access
- Export citation
The combinatorics of
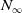 $N_\infty$ operads for
$N_\infty$ operads for 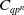 $C_{qp^n}$ and
$C_{qp^n}$ and 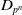 $D_{p^n}$
$D_{p^n}$
-
- Journal:
- Glasgow Mathematical Journal / Volume 67 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 03 October 2024, pp. 50-66
- Print publication:
- January 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ETS volume 44 issue 11 Cover and Front matter
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 11 / November 2024
- Published online by Cambridge University Press:
- 03 October 2024, pp. f1-f2
- Print publication:
- November 2024
-
- Article
-
- You have access
- Export citation
Classification of multiplication modules over multiplication rings with finitely many minimal primes
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 67 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 03 October 2024, pp. 67-71
- Print publication:
- January 2025
-
- Article
- Export citation
Volume and Euler classes in bounded cohomology of transformation groups
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 67 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 02 October 2024, pp. 34-49
- Print publication:
- January 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
PRM volume 154 issue 5 Cover and Back matter
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 5 / October 2024
- Published online by Cambridge University Press:
- 09 October 2024, pp. b1-b2
- Print publication:
- October 2024
-
- Article
-
- You have access
- Export citation
JAZ volume 117 issue 2 Cover and Back matter
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 117 / Issue 2 / October 2024
- Published online by Cambridge University Press:
- 09 October 2024, pp. b1-b2
- Print publication:
- October 2024
-
- Article
-
- You have access
- Export citation
JAZ volume 117 issue 2 Cover and Front matter
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 117 / Issue 2 / October 2024
- Published online by Cambridge University Press:
- 09 October 2024, pp. f1-f2
- Print publication:
- October 2024
-
- Article
-
- You have access
- Export citation
ETS volume 44 issue 10 Cover and Front matter
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 10 / October 2024
- Published online by Cambridge University Press:
- 01 October 2024, pp. f1-f2
- Print publication:
- October 2024
-
- Article
-
- You have access
- Export citation
PRM volume 154 issue 5 Cover and Front matter
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 5 / October 2024
- Published online by Cambridge University Press:
- 09 October 2024, pp. f1-f2
- Print publication:
- October 2024
-
- Article
-
- You have access
- Export citation
ETS volume 44 issue 10 Cover and Back matter
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 10 / October 2024
- Published online by Cambridge University Press:
- 01 October 2024, pp. b1-b2
- Print publication:
- October 2024
-
- Article
-
- You have access
- Export citation
Marked length pattern rigidity for arithmetic manifolds
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 4 / April 2025
- Published online by Cambridge University Press:
- 30 September 2024, pp. 1199-1223
- Print publication:
- April 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Uniform Diophantine approximation and run-length function in continued fractions
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 4 / April 2025
- Published online by Cambridge University Press:
- 30 September 2024, pp. 1246-1280
- Print publication:
- April 2025
-
- Article
- Export citation
Birkhoff attractors of dissipative billiards
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 4 / April 2025
- Published online by Cambridge University Press:
- 30 September 2024, pp. 989-1047
- Print publication:
- April 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Rank-one non-singular actions of countable groups and their odometer factors
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 4 / April 2025
- Published online by Cambridge University Press:
- 30 September 2024, pp. 1078-1128
- Print publication:
- April 2025
-
- Article
- Export citation
Hyperbolic actions of higher rank lattices come from rank-one factors
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 4 / April 2025
- Published online by Cambridge University Press:
- 30 September 2024, pp. 961-988
- Print publication:
- April 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On algebraic dependencies between Poincaré functions
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 3 / March 2025
- Published online by Cambridge University Press:
- 30 September 2024, pp. 915-935
- Print publication:
- March 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Weyl chamber length compactification of the
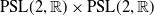 $\textrm{PSL}(2,{\mathbb{R}})\times \textrm{PSL}(2,{\mathbb{R}})$ maximal character variety
$\textrm{PSL}(2,{\mathbb{R}})\times \textrm{PSL}(2,{\mathbb{R}})$ maximal character variety
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 67 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 27 September 2024, pp. 11-33
- Print publication:
- January 2025
-
- Article
- Export citation
A parameter ASIP for the quadratic family
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 3 / March 2025
- Published online by Cambridge University Press:
- 24 September 2024, pp. 663-703
- Print publication:
- March 2025
-
- Article
- Export citation
PRODUCTION OPTIMIZATION FOR AGENTS OF DIFFERING WORK RATES
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 66 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 24 September 2024, pp. 98-120
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
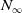
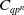
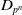




















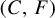
 of cofinite subgroups in
of cofinite subgroups in 
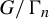


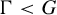
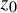

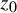
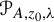 meromorphic on
meromorphic on 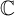
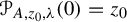 ,
, 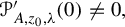 and
and 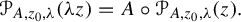 In this paper, we study the following problem: given Poincaré functions
In this paper, we study the following problem: given Poincaré functions 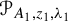 and
and 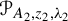 , find out if there is an algebraic relation
, find out if there is an algebraic relation 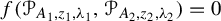 between them and, if such a relation exists, describe the corresponding algebraic curve
between them and, if such a relation exists, describe the corresponding algebraic curve