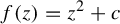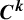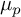Refine search
Actions for selected content:
28969 results in Differential and integral equations, dynamical systems and control theory
5 - Integral Fractional Laplacian in Unbounded Domains
-
- Book:
- Spectral and Spectral Element Methods for Fractional Ordinary and Partial Differential Equations
- Published online:
- 31 October 2024
- Print publication:
- 14 November 2024, pp 444-484
-
- Chapter
- Export citation
6 - Fractional Laplacian in Bounded Domains
-
- Book:
- Spectral and Spectral Element Methods for Fractional Ordinary and Partial Differential Equations
- Published online:
- 31 October 2024
- Print publication:
- 14 November 2024, pp 485-579
-
- Chapter
- Export citation
Frontmatter
-
- Book:
- Spectral and Spectral Element Methods for Fractional Ordinary and Partial Differential Equations
- Published online:
- 31 October 2024
- Print publication:
- 14 November 2024, pp i-vi
-
- Chapter
- Export citation
Exact dimension functions of the prime continued fraction Cantor set
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 6 / June 2025
- Published online by Cambridge University Press:
- 14 November 2024, pp. 1757-1776
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
7 - Time-Integration of Fractional Models
-
- Book:
- Spectral and Spectral Element Methods for Fractional Ordinary and Partial Differential Equations
- Published online:
- 31 October 2024
- Print publication:
- 14 November 2024, pp 580-652
-
- Chapter
- Export citation
Finite data rigidity for one-dimensional expanding maps
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 5 / May 2025
- Published online by Cambridge University Press:
- 13 November 2024, pp. 1597-1618
- Print publication:
- May 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On invariant measures of ‘satellite’ infinitely renormalizable quadratic polynomials
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 6 / June 2025
- Published online by Cambridge University Press:
- 13 November 2024, pp. 1843-1869
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Quantitative reducibility of
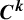 ${\boldsymbol {C}^{\boldsymbol {k}}}$ quasi-periodic cocycles
${\boldsymbol {C}^{\boldsymbol {k}}}$ quasi-periodic cocycles
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 6 / June 2025
- Published online by Cambridge University Press:
- 13 November 2024, pp. 1649-1672
- Print publication:
- June 2025
-
- Article
- Export citation
ARBITRARILY LARGE p-TORSION IN TATE-SHAFAREVICH GROUPS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 2 / March 2025
- Published online by Cambridge University Press:
- 12 November 2024, pp. 481-502
- Print publication:
- March 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON ODA’S PROBLEM AND SPECIAL LOCI
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 2 / March 2025
- Published online by Cambridge University Press:
- 12 November 2024, pp. 503-539
- Print publication:
- March 2025
-
- Article
- Export citation
Recent kernel methods for interacting particle systems: first numerical results
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 36 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 11 November 2024, pp. 464-489
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Hopf bifurcations for a delayed discrete single population patch model in advective environments
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 36 / Issue 4 / August 2025
- Published online by Cambridge University Press:
- 11 November 2024, pp. 705-737
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
AN EXAMPLE OF THE JANTZEN FILTRATION OF A D-MODULE
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 118 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 11 November 2024, pp. 265-296
- Print publication:
- June 2025
-
- Article
- Export citation
THE PRODUCT OF A GENERALIZED QUATERNION GROUP AND A CYCLIC GROUP
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 118 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 11 November 2024, pp. 31-64
- Print publication:
- February 2025
-
- Article
- Export citation
Global stability for McKean–Vlasov equations on large networks
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 08 November 2024, pp. 1-19
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A free boundary model for transport-induced neurite growth
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 36 / Issue 4 / August 2025
- Published online by Cambridge University Press:
- 07 November 2024, pp. 829-855
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
REDUCED QUIVER QUANTUM TOROIDAL ALGEBRAS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 2 / March 2025
- Published online by Cambridge University Press:
- 07 November 2024, pp. 341-369
- Print publication:
- March 2025
-
- Article
- Export citation
RATIONAL REPRESENTATIONS AND RATIONAL GROUP ALGEBRA OF VZ
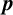 $\boldsymbol {p}$-GROUPS
$\boldsymbol {p}$-GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 118 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 06 November 2024, pp. 1-30
- Print publication:
- February 2025
-
- Article
- Export citation
Intersective sets for sparse sets of integers
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 5 / May 2025
- Published online by Cambridge University Press:
- 06 November 2024, pp. 1370-1402
- Print publication:
- May 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Dimension estimates for badly approximable affine forms
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 5 / May 2025
- Published online by Cambridge University Press:
- 06 November 2024, pp. 1541-1596
- Print publication:
- May 2025
-
- Article
- Export citation