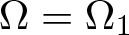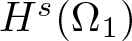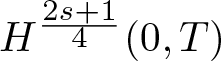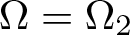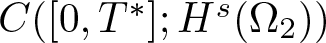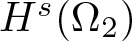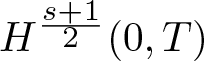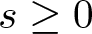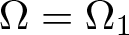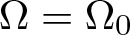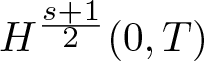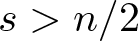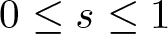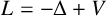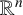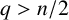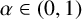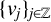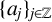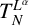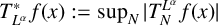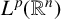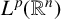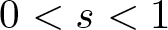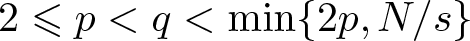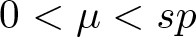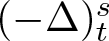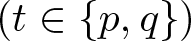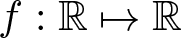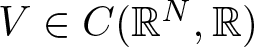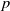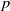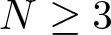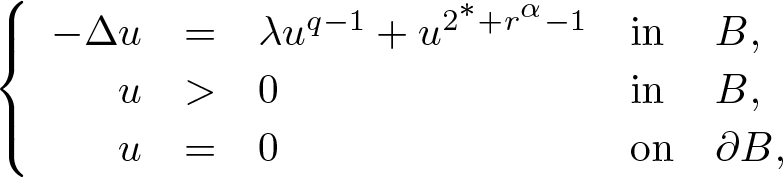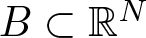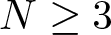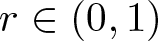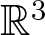Refine search
Actions for selected content:
28962 results in Differential and integral equations, dynamical systems and control theory
RIGIDITY FOR VON NEUMANN ALGEBRAS OF GRAPH PRODUCT GROUPS II. SUPERRIGIDITY RESULTS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 25 November 2024, pp. 117-156
- Print publication:
- January 2025
-
- Article
- Export citation
An MBO method for modularity optimisation based on total variation and signless total variation
- Part of
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 25 November 2024, pp. 1-83
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Enlargements and Morita contexts for rings with involution
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 67 / Issue 2 / May 2025
- Published online by Cambridge University Press:
- 25 November 2024, pp. 131-162
- Print publication:
- May 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On Riemann–Hilbert problem and multiple high-order pole solutions to the cubic Camassa–Holm equation
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 25 November 2024, pp. 1-51
-
- Article
- Export citation
Dynamics of projectable functions: towards an atlas of wandering domains for a family of Newton maps
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 25 November 2024, pp. 1-50
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Radial solutions of initial boundary value problems of nonlinear Schrödinger equations in ℝn
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 25 November 2024, pp. 1-55
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
BOUNDEDNESS OF DIFFERENTIAL TRANSFORMS FOR FRACTIONAL HEAT SEMIGROUPS GENERATED BY SCHRÖDINGER OPERATORS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 118 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 25 November 2024, pp. 210-244
- Print publication:
- April 2025
-
- Article
- Export citation
Commutativity properties of Quinn spectra
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 6 / December 2024
- Published online by Cambridge University Press:
- 25 November 2024, pp. 1848-1936
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Global dynamics for the stochastic nonlinear beam equations on the four-dimensional torus
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 25 November 2024, pp. 1-39
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Concentration and multiplicity of solutions for fractional double phase problems
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 25 November 2024, pp. 1-54
-
- Article
- Export citation
Improvement of some discrete Hardy inequalities with variants
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 67 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 25 November 2024, pp. 114-130
- Print publication:
- January 2025
-
- Article
- Export citation
The effect of a perturbation on Brezis-Nirenberg’s problem
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 25 November 2024, pp. 1-16
-
- Article
- Export citation
Equivalence between the functional equation and Voronoï-type summation identities for a class of L-functions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 25 November 2024, pp. 1-41
-
- Article
- Export citation
Pullback measure attractors for non-autonomous stochastic lattice systems
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 22 November 2024, pp. 1-20
-
- Article
- Export citation
Fence of saddle solutions of the Allen–Cahn equation in the plane
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 22 November 2024, pp. 1-42
-
- Article
- Export citation
A criterion to detect a non-trivial homology of an invariant set of a flow in
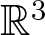 $\mathbb{R}^3$
$\mathbb{R}^3$
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 22 November 2024, pp. 1-31
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A remark on the well-posedness of the modified KdV equation in L2
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 22 November 2024, pp. 1-26
-
- Article
- Export citation
Equivariant covering type and the number of vertices in equivariant triangulations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 22 November 2024, pp. 1-32
-
- Article
- Export citation
Random walks on groups and superlinear-divergent geodesics
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 5 / May 2025
- Published online by Cambridge University Press:
- 21 November 2024, pp. 1403-1443
- Print publication:
- May 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Entropy of group actions beyond uniform lattices
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 5 / May 2025
- Published online by Cambridge University Press:
- 21 November 2024, pp. 1461-1502
- Print publication:
- May 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation