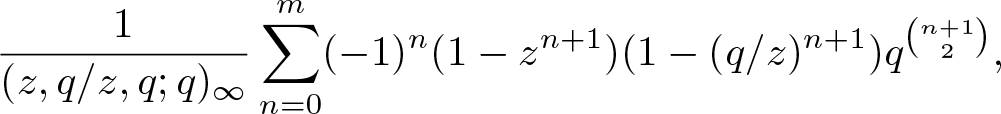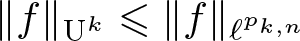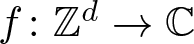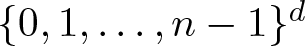Refine search
Actions for selected content:
28927 results in Differential and integral equations, dynamical systems and control theory
JMJ volume 24 issue 4 Cover and Front matter
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 4 / July 2025
- Published online by Cambridge University Press:
- 23 June 2025, pp. f1-f2
- Print publication:
- July 2025
-
- Article
-
- You have access
- Export citation
Truncated Jacobi triple product series II: Li, Lin, and Wang’s nonnegativity conjecture
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 19 June 2025, pp. 1-15
-
- Article
- Export citation
Optimal function spaces in weighted Sobolev embeddings with α-homogeneous weights
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 19 June 2025, pp. 1-30
-
- Article
- Export citation
Topological structure of isolated points in the space of
 $\mathbb {Z}^d$-shifts
$\mathbb {Z}^d$-shifts
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 11 / November 2025
- Published online by Cambridge University Press:
- 18 June 2025, pp. 3344-3376
- Print publication:
- November 2025
-
- Article
- Export citation
Sharp estimates for Gowers norms on discrete cubes
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 16 June 2025, pp. 1-27
-
- Article
- Export citation
MIRROR SYMMETRY FOR TROPICAL HYPERSURFACES AND PATCHWORKING
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu , First View
- Published online by Cambridge University Press:
- 11 June 2025, pp. 1-39
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On Dirichlet non-improvable numbers and shrinking target problems
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 11 / November 2025
- Published online by Cambridge University Press:
- 11 June 2025, pp. 3540-3568
- Print publication:
- November 2025
-
- Article
- Export citation
Phragmén–Lindelöf principles and Julia limiting directions of quasiregular mappings
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 11 / November 2025
- Published online by Cambridge University Press:
- 11 June 2025, pp. 3325-3343
- Print publication:
- November 2025
-
- Article
- Export citation
RIGIDITY FOR VON NEUMANN ALGEBRAS OF GRAPH PRODUCT GROUPS II. SUPERRIGIDITY RESULTS - ADDENDUM
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu , First View
- Published online by Cambridge University Press:
- 11 June 2025, p. 1
-
- Article
- Export citation
Dynamics of generic automorphisms of Stein manifolds with the density property
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 11 / November 2025
- Published online by Cambridge University Press:
- 09 June 2025, pp. 3305-3324
- Print publication:
- November 2025
-
- Article
- Export citation
ALGEBRAIC DYNAMICAL SYSTEMS FROM LDPC CODES SATISFY A STRONG NEGATION OF THE WEAK PINSKER PROPERTY
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu , First View
- Published online by Cambridge University Press:
- 09 June 2025, pp. 1-69
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On quasiconformal non-equivalence of gasket Julia sets and limit sets
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 11 / November 2025
- Published online by Cambridge University Press:
- 09 June 2025, pp. 3465-3489
- Print publication:
- November 2025
-
- Article
- Export citation
Part Two - Partial Differential Equations
-
- Book:
- Notes, Problems and Solutions in Differential Equations
- Published online:
- 15 April 2025
- Print publication:
- 05 June 2025, pp 183-184
-
- Chapter
- Export citation
Frontmatter
-
- Book:
- Notes, Problems and Solutions in Differential Equations
- Published online:
- 15 April 2025
- Print publication:
- 05 June 2025, pp i-iv
-
- Chapter
- Export citation
3 - Series Solutions: Frobenius Theory
-
- Book:
- Notes, Problems and Solutions in Differential Equations
- Published online:
- 15 April 2025
- Print publication:
- 05 June 2025, pp 85-110
-
- Chapter
- Export citation
Part One - Ordinary Differential Equations
-
- Book:
- Notes, Problems and Solutions in Differential Equations
- Published online:
- 15 April 2025
- Print publication:
- 05 June 2025, pp 1-2
-
- Chapter
- Export citation
10 - One-Dimensional Wave Equation
-
- Book:
- Notes, Problems and Solutions in Differential Equations
- Published online:
- 15 April 2025
- Print publication:
- 05 June 2025, pp 307-328
-
- Chapter
- Export citation
Dedication
-
- Book:
- Notes, Problems and Solutions in Differential Equations
- Published online:
- 15 April 2025
- Print publication:
- 05 June 2025, pp v-vi
-
- Chapter
- Export citation
Notation
-
- Book:
- Notes, Problems and Solutions in Differential Equations
- Published online:
- 15 April 2025
- Print publication:
- 05 June 2025, pp xvii-xx
-
- Chapter
- Export citation
2 - Linear Systems
-
- Book:
- Notes, Problems and Solutions in Differential Equations
- Published online:
- 15 April 2025
- Print publication:
- 05 June 2025, pp 47-84
-
- Chapter
- Export citation