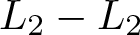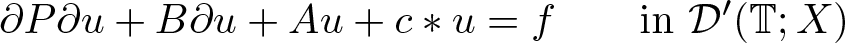Refine search
Actions for selected content:
28929 results in Differential and integral equations, dynamical systems and control theory
Local well-posedness and blow-up in the energy space for the 2D NLS with point interaction
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 11 July 2025, pp. 1-20
-
- Article
- Export citation
The moving plane method and the uniqueness of high-order elliptic equation with GJMS operator
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 10 July 2025, pp. 1-45
-
- Article
- Export citation
Regular solutions to the dissipative Aw–Rascle system
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 10 July 2025, pp. 1-33
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Sub-additivity of measure theoretic entropies of commuting transformations on Banach spaces
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 11 / November 2025
- Published online by Cambridge University Press:
- 10 July 2025, pp. 3430-3464
- Print publication:
- November 2025
-
- Article
- Export citation
log-Hölder continuity of the rotation number
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 08 July 2025, pp. 1-11
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SPECIAL RICCI–HESSIAN EQUATIONS ON KÄHLER MANIFOLDS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 07 July 2025, pp. 1-21
-
- Article
- Export citation
JAZ volume 119 issue 1 Cover and Back matter
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 119 / Issue 1 / August 2025
- Published online by Cambridge University Press:
- 07 July 2025, pp. b1-b3
- Print publication:
- August 2025
-
- Article
-
- You have access
- Export citation
SPATIAL PATTERN FORMATION IN A MODEL OF THE BRAY–LIEBHAFSKY REACTION
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 67 / 2025
- Published online by Cambridge University Press:
- 07 July 2025, e24
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
JAZ volume 119 issue 1 Cover and Front matter
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 119 / Issue 1 / August 2025
- Published online by Cambridge University Press:
- 07 July 2025, pp. f1-f2
- Print publication:
- August 2025
-
- Article
-
- You have access
- Export citation
SIAMESE NETWORKS FOR POINCARÉ EMBEDDINGS AND THE RECONSTRUCTION OF EVOLUTIONARY TREES
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 67 / 2025
- Published online by Cambridge University Press:
- 07 July 2025, e25
-
- Article
- Export citation
Global boundedness and stabilization of solutions for a chemotaxis system with acceleration and logistic source
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 04 July 2025, pp. 1-30
-
- Article
- Export citation
The evolution problem for the 1D nonlocal Fisher-KPP equation with a top hat kernel. Part 2. The initial-boundary value problem on a finite domain
- Part of
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 04 July 2025, pp. 1-31
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ETS volume 45 issue 8 Cover and Back matter
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 8 / August 2025
- Published online by Cambridge University Press:
- 03 July 2025, pp. b1-b2
- Print publication:
- August 2025
-
- Article
-
- You have access
- Export citation
ETS volume 45 issue 8 Cover and Front matter
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 8 / August 2025
- Published online by Cambridge University Press:
- 03 July 2025, pp. f1-f2
- Print publication:
- August 2025
-
- Article
-
- You have access
- Export citation
On non-tameness of the Ellis semigroup
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 11 / November 2025
- Published online by Cambridge University Press:
- 30 June 2025, pp. 3419-3429
- Print publication:
- November 2025
-
- Article
- Export citation

Probability, Geometry and Integrable Systems
-
- Published online:
- 27 June 2025
- Print publication:
- 17 March 2008

Inside Out
- Inverse Problems and Applications
-
- Published online:
- 26 June 2025
- Print publication:
- 10 November 2003
EDITORIAL: AT THE FRONTIER OF APPLIED DYNAMICAL SYSTEMS SPECIAL ISSUE IN HONOUR OF PROFESSOR BERND KRAUSKOPF (On the occasion of his 60th birthday)
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 67 / 2025
- Published online by Cambridge University Press:
- 25 June 2025, e23
-
- Article
-
- You have access
- HTML
- Export citation
ARITHMETIC SPECIAL CYCLES AND JACOBI FORMS
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu , First View
- Published online by Cambridge University Press:
- 25 June 2025, pp. 1-35
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The invariant subspaces of periodic Fourier multipliers with application to abstract evolution equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 24 June 2025, pp. 1-47
-
- Article
- Export citation