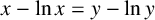Refine search
Actions for selected content:
8126 results in Fluid dynamics and solid mechanics
INFLUENCE OF NOISE-INDUCED MODULATIONS ON THE TIMING STABILITY OF PASSIVELY MODE-LOCKED SEMICONDUCTOR LASER SUBJECT TO OPTICAL FEEDBACK
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 67 / 2025
- Published online by Cambridge University Press:
- 29 May 2025, e22
-
- Article
- Export citation
ALPHA–DELTA TRANSITIONS IN CORTICAL RHYTHMS AS GRAZING BIFURCATIONS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 67 / 2025
- Published online by Cambridge University Press:
- 21 May 2025, e21
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
BIFURCATION ANALYSIS OF THE EFFECT OF TYRE INFLATION PRESSURE ON WHEEL SHIMMY WITH MULTIPLE TYRE PROPERTIES CONSIDERED
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 67 / 2025
- Published online by Cambridge University Press:
- 16 May 2025, e20
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
DELAYED HOPF BIFURCATIONS IN REACTION–DIFFUSION SYSTEMS IN TWO SPACE DIMENSIONS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 67 / 2025
- Published online by Cambridge University Press:
- 13 May 2025, e19
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
MULTIPLE LOCAL AND GLOBAL BIFURCATIONS AND THEIR ROLE IN QUORUM SENSING DYNAMICS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 67 / 2025
- Published online by Cambridge University Press:
- 09 April 2025, e17
-
- Article
- Export citation
GENERIC PLANAR PHASE RESETTING NEAR A PHASELESS POINT
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 67 / 2025
- Published online by Cambridge University Press:
- 08 April 2025, e18
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
MIXED BOUNDARY VALUE PROBLEM IN MICROFLUIDICS: THE AVER’YANOV–BLUNT MODEL REVISITED
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 67 / 2025
- Published online by Cambridge University Press:
- 07 April 2025, e16
-
- Article
-
- You have access
- Open access
- HTML
- Export citation

Topographic Effects in Stratified Flows
-
- Published online:
- 04 April 2025
- Print publication:
- 27 January 2022
PERIODIC SOLUTIONS FOR A PAIR OF DELAY-COUPLED ACTIVE THETA NEURONS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 67 / 2025
- Published online by Cambridge University Press:
- 03 April 2025, e11
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ANALYTICAL APPROXIMATIONS OF LOTKA–VOLTERRA INTEGRALS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 67 / 2025
- Published online by Cambridge University Press:
- 02 April 2025, e10
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
DYNAMICAL ANALYSIS OF A PARAMETRICALLY FORCED MAGNETO-MECHANICAL OSCILLATOR
-
- Journal:
- The ANZIAM Journal / Volume 67 / 2025
- Published online by Cambridge University Press:
- 02 April 2025, e15
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ANALYSIS OF A DISCRETIZED FRACTIONAL-ORDER PREY–PREDATOR MODEL UNDER WIND EFFECT
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 67 / 2025
- Published online by Cambridge University Press:
- 02 April 2025, e9
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ESTIMATION OF MEAN SQUARED ERRORS OF NON-BINARY A/D ENCODERS THROUGH FREDHOLM DETERMINANTS OF PIECEWISE-LINEAR TRANSFORMATIONS II: GENERAL CASE
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 67 / 2025
- Published online by Cambridge University Press:
- 19 March 2025, e14
-
- Article
- Export citation
MICRO-MACRO PARAREAL, FROM ORDINARY DIFFERENTIAL EQUATIONS TO STOCHASTIC DIFFERENTIAL EQUATIONS AND BACK AGAIN
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 67 / 2025
- Published online by Cambridge University Press:
- 17 March 2025, e13
-
- Article
- Export citation
A SIXTH-ORDER HERMITE COLLOCATION TECHNIQUE FOR NUMERICAL STUDY OF NONLINEAR FISHER AND BURGERS–FISHER EQUATIONS
-
- Journal:
- The ANZIAM Journal / Volume 67 / 2025
- Published online by Cambridge University Press:
- 14 March 2025, e12
-
- Article
- Export citation

Fundamentals of Transport Processes with Applications
-
- Published online:
- 28 February 2025
- Print publication:
- 16 February 2023
-
- Textbook
- Export citation
CONFORMAL IMAGE REGISTRATION USING THE DISCRETIZED CAUCHY–RIEMANN EQUATIONS
-
- Journal:
- The ANZIAM Journal / Volume 67 / 2025
- Published online by Cambridge University Press:
- 18 February 2025, e8
-
- Article
- Export citation
INDEX
-
- Journal:
- The ANZIAM Journal / Volume 66 / Issue 4 / October 2024
- Published online by Cambridge University Press:
- 12 February 2025, pp. 285-286
-
- Article
- Export citation
Contents
-
- Book:
- Coarse Graining Turbulence
- Published online:
- 31 January 2025
- Print publication:
- 06 February 2025, pp v-xi
-
- Chapter
- Export citation
8 - Verification, Validation, Uncertainty Quantification, and Coarse-Graining
- from Part I - Paradigms and Tools
-
-
- Book:
- Coarse Graining Turbulence
- Published online:
- 31 January 2025
- Print publication:
- 06 February 2025, pp 222-260
-
- Chapter
- Export citation