In this paper some existence results for third-order differential equations with nonlinear boundary value conditions are derived. Functional dependence in the data is allowed. In the proofs we use the method of upper and lower solutions, Schauder's fixed point theorem and results from Cabada and Heikkilä on third-order differential equations with linear and nonfunctional initial-boundary value conditions.

Some initial value problems are considered which arise in the treatment of a one-dimensional gas of point particles interacting with a “hard-core” potential.

Two basic types of initial conditions are considered. For the first, one particle is specified to be at the origin with a given velocity. The positions in phase space of the remaining background of particles are represented by continuous distribution functions. The second problem is a periodic analogue of the first.

Exact equations for the delta-function part of the single particle distribution functions are derived for the non-periodic case and approximate equations for the periodic case. These take the form of differential operator equations. The spectral and asymptotic properties of the operators associated with the two cases are examined and compared. The behaviour of the solutions is also considered.

The modelling of the combustion of dust suspensions leads to a nonlinear eigenvalue problem for a system of ordinary differential equations defined over an infinite interval. The equations contain a number of parameters. In this study, the shooting method is used to prove the existence of a solution. Linearisation is then used to provide an approximate solution, from which an estimate of the eigenvalue and its dependence on the given parameters can be obtained.

The evolution of small amplitude waves on an open two layer fluid is investigated. The spatially periodic surface and interface displacements are represented as Fourier series with time dependent coefficients, for which evolution equations with all significant quadratic interactions included, are derived. Solutions to these equations are found analytically for a small number of harmonics, and numerically for a larger number of harmonics. Two numerical solutions are given to illustrate the evolution properties.

The Sharpe-Lotka-McKendrick (or von Foerster) equations for an age-structured population, with a nonlinear term to represent overcrowding or competition for resources, are considered. The model is extended to include a growth term, allowing the population to be structured by size or weight rather than age, and a general solution is presented. Various examples are then considered, including the case of cell growth where cells divide at a given size.

This is an application of the characteristic identity satisfied by matrices whose elements are also elements of a semi-simple Lie algebra. Generalized eigenvectors are determined for matrices consisting of generators of GL(n), O(n) and Sp(n), and it is shown how to resolve the identity into idempotents constructed from such eigenvectors. By this means rather general functions of the matrices may be defined. It is also shown how to determine traces of such functions, in terms of the invariants of the Lie algebra.

We prove the existence of optimal control for nonlinear systems having implicit derivative with quadratic performace criteria.

The singularity subtraction technique described by Kantorovich and Krylov in [11] is designed to reduce or overcome the effect of a weakly singular kernel in the numerical solution of integral equations. First, the equation is rearranged in such a way that the singularity of the kernel is at least partially cancelled by the smoothness of the solution, and then numerical integration is applied. We present convergence results and error bounds under general conditions on the nature of the singularity and the numerical integration procedure. Numerical examples demonstrate the benefit of the singularity subtraction technique.

The velocities of Rayleigh surface waves and, when they exist, Stoneley interface waves can be obtained as the roots of two irrational functions. Here previous results are extended by using standard operations related to the Wiener-Hopf technique to provide expressions in quadrature for these roots.

Stochastic Petri Nets are used extensively to find performance measures for communication protocols. This paper illustrates how equilibrium distributions for the markings of a wide class of nets can be found directly without the need to generate a large state space and then resort to equilibrium balance equations.

We discuss uniqueness and continuation of solutions to the Cauchy problem for a two dimensional Emden-Fowler differential system.

The method of generalized cross-validation (GCV) provides a good value for the “ridge” regularization parameter for an ill-conditioned linear system, such as the system produced by discretization of a Fredholm integral equation of the first kind. In this note we apply GCV to a wider class of estimators than the one parameter ridge estimators. We observe that the expected values of the parameter mean-square error, the predictive mean-square error, and the GCV function are simultaneously minimized over this new class, so we accept the minimizer of the GCV function as the best computable estimator. We present a simple algorithm for computing this estimator from the data, so that a numerical search is not needed.

Consider the nonlinear neutral equation

where pi(t), hi(t), gj(t), Q(t) Є C[t0, ∞), limt→∞hi(t) = ∞, limt→∞gj(t) = ∞ i Є Im = {1, 2, …, m}, j Є In = {1, 2, …, n}. We obtain a necessary and sufficient condition (2) for this equation to have a nonoscillatory solution x(t) with limt→∞ inf|x(t)| > 0 (Theorems 5 and 6) or to have a bounded nonoscillatory solution x(t) with limt→∞ inf|x(t)| > 0 (Theorem 7).

Within the scope of Eringen's linearised micropolar theory, this note outlines a solution for the stress concentration around an elliptic hole in an infinite plate under axial tension.

We consider the phase-locked solutions of the differential equation governing planar motion of a weakly damped pendulum forced by a prescribed, vertical acceleration εg sin ωt of its pivot, where ω and t are dimensionless, and the unit of time is the reciprocal of the natural frequency. Resonance curves and stability boundaries are presented for downward and inverted oscillations of periods T, 2T, 4T, …, where T (≡ 2π/ω) is the forcing period. Stable, downward oscillations are found to occur in distinct regions of the (ω, ε) plane, reminiscent of the regions of stability of the Mathieu equation (which describes the equivalent undamped, parametrically excited pendulum motion). 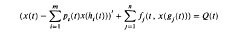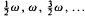The regions are dominated by oscillations of frequencies , each region being bounded on one side by a vertical state at rest in stable equilibrium and on the other side by a symmetry-breaking, period-doubling sequence to chaotic motion. Stable, inverted oscillations are found to occur also in distinct regions of the (ω, ε) plane, the principal oscillation in each region being symmetric with period 2T.

A method based on the minimization of variation is presented for the identification of a completely unknown blur operator. We assume the knowledge of a blurred image and its original version. The class of blurring operators is identified in the class of compact operators. A variational method with negative norms is then used for the restoration of a blurred and noised image. The restoration method works for a wide class of blurring operators and we do not assume that the blur operator commutes with the Laplacian.