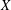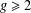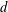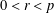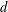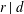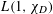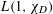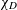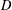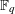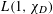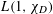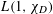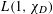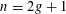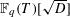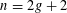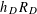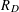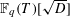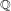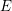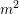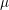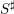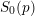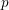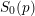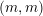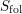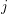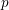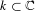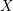Refine listing
Actions for selected content:
361 results in 14Gxx
Logarithmes des points rationnels des variétés abéliennes
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 2 / April 2019
- Published online by Cambridge University Press:
- 09 January 2019, pp. 247-298
- Print publication:
- April 2019
-
- Article
-
- You have access
- Export citation
ON MAXIMALLY FROBENIUS DESTABILISED VECTOR BUNDLES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 2 / April 2019
- Published online by Cambridge University Press:
- 04 January 2019, pp. 195-202
- Print publication:
- April 2019
-
- Article
-
- You have access
- Export citation
Mean values of derivatives of L-functions in function fields: III
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 4 / August 2019
- Published online by Cambridge University Press:
- 27 December 2018, pp. 905-913
- Print publication:
- August 2019
-
- Article
- Export citation
COMPLEX MOMENTS AND THE DISTRIBUTION OF VALUES OF
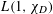 $L(1,\unicode[STIX]{x1D712}_{D})$ OVER FUNCTION FIELDS WITH APPLICATIONS TO CLASS NUMBERS
$L(1,\unicode[STIX]{x1D712}_{D})$ OVER FUNCTION FIELDS WITH APPLICATIONS TO CLASS NUMBERS
- Part of
-
- Journal:
- Mathematika / Volume 65 / Issue 2 / 2019
- Published online by Cambridge University Press:
- 05 December 2018, pp. 236-271
- Print publication:
- 2019
-
- Article
- Export citation
On the Frequency of Algebraic Brauer Classes on Certain Log K3 Surfaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 3 / September 2019
- Published online by Cambridge University Press:
- 03 December 2018, pp. 551-563
- Print publication:
- September 2019
-
- Article
-
- You have access
- Export citation
ZERO-LOCI OF BRAUER GROUP ELEMENTS ON SEMI-SIMPLE ALGEBRAIC GROUPS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 5 / September 2020
- Published online by Cambridge University Press:
- 29 November 2018, pp. 1467-1507
- Print publication:
- September 2020
-
- Article
- Export citation
A motivic version of the theorem of Fontaine and Wintenberger
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 1 / January 2019
- Published online by Cambridge University Press:
- 23 November 2018, pp. 38-88
- Print publication:
- January 2019
-
- Article
- Export citation
Constancy of generalized Hodge–Tate weights of a local system
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 12 / December 2018
- Published online by Cambridge University Press:
- 06 November 2018, pp. 2606-2642
- Print publication:
- December 2018
-
- Article
- Export citation
MOTIVIC HILBERT ZETA FUNCTIONS OF CURVES ARE RATIONAL
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 3 / May 2020
- Published online by Cambridge University Press:
- 31 October 2018, pp. 947-964
- Print publication:
- May 2020
-
- Article
- Export citation
Foliations on unitary Shimura varieties in positive characteristic
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 11 / November 2018
- Published online by Cambridge University Press:
- 11 October 2018, pp. 2267-2304
- Print publication:
- November 2018
-
- Article
- Export citation
HIGHER IDELES AND CLASS FIELD THEORY
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 236 / December 2019
- Published online by Cambridge University Press:
- 02 October 2018, pp. 214-250
- Print publication:
- December 2019
-
- Article
-
- You have access
- HTML
- Export citation
RAPOPORT–ZINK UNIFORMIZATION OF HODGE-TYPE SHIMURA VARIETIES
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 6 / 2018
- Published online by Cambridge University Press:
- 03 September 2018, e16
-
- Article
-
- You have access
- Open access
- Export citation
Applications of the hyperbolic Ax–Schanuel conjecture
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 9 / September 2018
- Published online by Cambridge University Press:
- 13 August 2018, pp. 1843-1888
- Print publication:
- September 2018
-
- Article
- Export citation
The Manin constant in the semistable case
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 9 / September 2018
- Published online by Cambridge University Press:
- 13 August 2018, pp. 1889-1920
- Print publication:
- September 2018
-
- Article
- Export citation
COMPARING THE BRAUER GROUP TO THE TATE–SHAFAREVICH GROUP
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 3 / May 2020
- Published online by Cambridge University Press:
- 19 July 2018, pp. 965-970
- Print publication:
- May 2020
-
- Article
- Export citation
A SIMPLE PROOF OF CHEBOTAREV’S DENSITY THEOREM OVER FINITE FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 2 / October 2018
- Published online by Cambridge University Press:
- 12 July 2018, pp. 196-202
- Print publication:
- October 2018
-
- Article
-
- You have access
- Export citation
INTEGRAL AND ADELIC ASPECTS OF THE MUMFORD–TATE CONJECTURE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 3 / May 2020
- Published online by Cambridge University Press:
- 07 June 2018, pp. 869-890
- Print publication:
- May 2020
-
- Article
- Export citation
Arithmetic intersection on GSpin Rapoport–Zink spaces
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 7 / July 2018
- Published online by Cambridge University Press:
- 16 May 2018, pp. 1407-1440
- Print publication:
- July 2018
-
- Article
- Export citation
Duality for relative logarithmic de Rham–Witt sheaves and wildly ramified class field theory over finite fields
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 6 / June 2018
- Published online by Cambridge University Press:
- 07 May 2018, pp. 1306-1331
- Print publication:
- June 2018
-
- Article
- Export citation
Approximation forte pour les variétés avec une action d’un groupe linéaire
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 4 / April 2018
- Published online by Cambridge University Press:
- 08 March 2018, pp. 773-819
- Print publication:
- April 2018
-
- Article
- Export citation