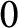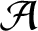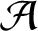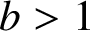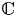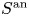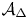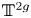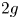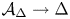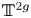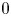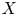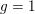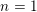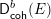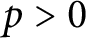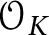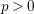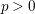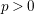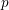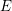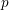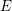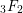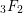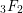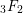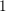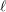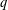Refine listing
Actions for selected content:
105 results in 14Kxx
Zariski dense orbits for regular self-maps on split semiabelian varieties
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 05 March 2021, pp. 116-122
- Print publication:
- March 2022
-
- Article
- Export citation
Rigid-analytic varieties with projective reduction violating Hodge symmetry
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 3 / March 2021
- Published online by Cambridge University Press:
- 19 March 2021, pp. 625-640
- Print publication:
- March 2021
-
- Article
- Export citation
CHARACTERISTIC POLYNOMIALS OF SIMPLE ORDINARY ABELIAN VARIETIES OVER FINITE FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 3 / December 2021
- Published online by Cambridge University Press:
- 19 February 2021, pp. 391-397
- Print publication:
- December 2021
-
- Article
- Export citation
Generic rank of Betti map and unlikely intersections
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 12 / December 2020
- Published online by Cambridge University Press:
- 12 January 2021, pp. 2469-2509
- Print publication:
- December 2020
-
- Article
- Export citation
CLASS NUMBERS OF CM ALGEBRAIC TORI, CM ABELIAN VARIETIES AND COMPONENTS OF UNITARY SHIMURA VARIETIES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 245 / March 2022
- Published online by Cambridge University Press:
- 28 October 2020, pp. 74-99
- Print publication:
- March 2022
-
- Article
- Export citation
Summands of theta divisors on Jacobians
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 7 / July 2020
- Published online by Cambridge University Press:
- 08 July 2020, pp. 1457-1475
- Print publication:
- July 2020
-
- Article
- Export citation
The bounded height conjecture for semiabelian varieties
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 7 / July 2020
- Published online by Cambridge University Press:
- 30 June 2020, pp. 1405-1456
- Print publication:
- July 2020
-
- Article
- Export citation
Computing a categorical Gromov–Witten invariant
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 7 / July 2020
- Published online by Cambridge University Press:
- 18 June 2020, pp. 1275-1309
- Print publication:
- July 2020
-
- Article
- Export citation
Faltings extension and Hodge-Tate filtration for abelian varieties over p-adic local fields with imperfect residue fields
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 11 June 2020, pp. 247-263
- Print publication:
- June 2021
-
- Article
- Export citation
ON VARIETIES WITH TRIVIAL TANGENT BUNDLE IN CHARACTERISTIC
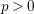 $p>0$
$p>0$
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 242 / June 2021
- Published online by Cambridge University Press:
- 26 June 2019, pp. 35-51
- Print publication:
- June 2021
-
- Article
- Export citation
Families of Picard modular forms and an application to the Bloch–Kato conjecture
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 7 / July 2019
- Published online by Cambridge University Press:
- 25 June 2019, pp. 1327-1401
- Print publication:
- July 2019
-
- Article
- Export citation
Primes Dividing Invariants of CM Picard Curves
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 07 May 2019, pp. 480-504
- Print publication:
- April 2020
-
- Article
-
- You have access
- Export citation
A FUNCTIONAL LOGARITHMIC FORMULA FOR THE HYPERGEOMETRIC FUNCTION
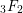 $_{3}F_{2}$
$_{3}F_{2}$
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 236 / December 2019
- Published online by Cambridge University Press:
- 14 September 2018, pp. 29-46
- Print publication:
- December 2019
-
- Article
-
- You have access
- HTML
- Export citation
AN ALGEBRO-GEOMETRIC STUDY OF SPECIAL VALUES OF HYPERGEOMETRIC FUNCTIONS
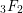 $_{3}F_{2}$
$_{3}F_{2}$
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 236 / December 2019
- Published online by Cambridge University Press:
- 13 September 2018, pp. 47-62
- Print publication:
- December 2019
-
- Article
-
- You have access
- HTML
- Export citation
Constructing elliptic curves from Galois representations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 10 / October 2018
- Published online by Cambridge University Press:
- 29 August 2018, pp. 2045-2054
- Print publication:
- October 2018
-
- Article
- Export citation
Arithmetical Power Series Expansion of the Sigma Function for a Plane Curve
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 4 / November 2018
- Published online by Cambridge University Press:
- 22 June 2018, pp. 995-1022
-
- Article
- Export citation
THETA BLOCK FOURIER EXPANSIONS, BORCHERDS PRODUCTS AND A SEQUENCE OF NEWMAN AND SHANKS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 1 / August 2018
- Published online by Cambridge University Press:
- 14 June 2018, pp. 48-59
- Print publication:
- August 2018
-
- Article
-
- You have access
- Export citation
DISTINGUISHED MODELS OF INTERMEDIATE JACOBIANS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 3 / May 2020
- Published online by Cambridge University Press:
- 08 June 2018, pp. 891-918
- Print publication:
- May 2020
-
- Article
- Export citation
UNIVERSAL COVERS OF COMMUTATIVE FINITE MORLEY RANK GROUPS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 3 / May 2020
- Published online by Cambridge University Press:
- 26 April 2018, pp. 767-799
- Print publication:
- May 2020
-
- Article
- Export citation
Abelian varieties isogenous to a power of an elliptic curve
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 5 / May 2018
- Published online by Cambridge University Press:
- 21 March 2018, pp. 934-959
- Print publication:
- May 2018
-
- Article
- Export citation