Refine listing
Actions for selected content:
105 results in 14Kxx
THE DISTRIBUTION OF TORSION SUBSCHEMES OF ABELIAN VARIETIES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 15 / Issue 4 / October 2016
- Published online by Cambridge University Press:
- 15 December 2014, pp. 693-710
- Print publication:
- October 2016
-
- Article
- Export citation
Explicit Kummer varieties of hyperelliptic Jacobian threefolds
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue 1 / 2014
- Published online by Cambridge University Press:
- 01 September 2014, pp. 496-508
-
- Article
-
- You have access
- Export citation
The non-existence of stable Schottky forms
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 4 / April 2014
- Published online by Cambridge University Press:
- 10 March 2014, pp. 679-690
- Print publication:
- April 2014
-
- Article
- Export citation
Singular values of multiple eta-quotients for ramified primes
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 16 / October 2013
- Published online by Cambridge University Press:
- 07 November 2013, pp. 407-418
-
- Article
-
- You have access
- Export citation
Determinants of subquotients of Galois representations associated with abelian varieties
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 13 / Issue 3 / July 2014
- Published online by Cambridge University Press:
- 18 July 2013, pp. 517-559
- Print publication:
- July 2014
-
- Article
- Export citation
Smash nilpotent cycles on varieties dominated by products of curves
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 9 / September 2013
- Published online by Cambridge University Press:
- 28 June 2013, pp. 1511-1518
- Print publication:
- September 2013
-
- Article
- Export citation
GENERIC VANISHING THEORY VIA MIXED HODGE MODULES
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 1 / 2013
- Published online by Cambridge University Press:
- 17 May 2013, e1
-
- Article
-
- You have access
- Open access
- Export citation
Corrigendum: Varieties with ample cotangent bundle (Compositio Math. 141 (2005), 1445–1459)
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 3 / March 2013
- Published online by Cambridge University Press:
- 28 February 2013, pp. 505-506
- Print publication:
- March 2013
-
- Article
- Export citation
Complete addition laws on abelian varieties
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 15 / May 2012
- Published online by Cambridge University Press:
- 01 September 2012, pp. 308-316
-
- Article
-
- You have access
- Export citation
Sato–Tate distributions and Galois endomorphism modules in genus 2
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 5 / September 2012
- Published online by Cambridge University Press:
- 25 July 2012, pp. 1390-1442
- Print publication:
- September 2012
-
- Article
-
- You have access
- Export citation
Computing isogenies between abelian varieties
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 5 / September 2012
- Published online by Cambridge University Press:
- 10 July 2012, pp. 1483-1515
- Print publication:
- September 2012
-
- Article
-
- You have access
- Export citation
Kummer surfaces and the computation of the Picard group
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 15 / May 2012
- Published online by Cambridge University Press:
- 01 April 2012, pp. 84-100
-
- Article
-
- You have access
- Export citation
Langlands duality and global Springer theory
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 3 / May 2012
- Published online by Cambridge University Press:
- 19 March 2012, pp. 835-867
- Print publication:
- May 2012
-
- Article
-
- You have access
- Export citation
Abelian functions associated with genus three algebraic curves
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 14 / 2011
- Published online by Cambridge University Press:
- 01 November 2011, pp. 291-326
-
- Article
-
- You have access
- Export citation
Some unlikely intersections beyond André–Oort
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 1 / January 2012
- Published online by Cambridge University Press:
- 30 August 2011, pp. 1-27
- Print publication:
- January 2012
-
- Article
-
- You have access
- Export citation
Families of explicitly isogenous Jacobians of variable-separated curves
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 14 / 2011
- Published online by Cambridge University Press:
- 01 August 2011, pp. 179-199
-
- Article
-
- You have access
- Export citation
Pseudoeffective and nef classes on abelian varieties
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 6 / November 2011
- Published online by Cambridge University Press:
- 01 June 2011, pp. 1793-1818
- Print publication:
- November 2011
-
- Article
-
- You have access
- Export citation
Supersingular Kottwitz–Rapoport strata and Deligne–Lusztig varieties
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 9 / Issue 2 / April 2010
- Published online by Cambridge University Press:
- 11 August 2009, pp. 357-390
- Print publication:
- April 2010
-
- Article
- Export citation
The affine part of the Picard scheme
- Part of
-
- Journal:
- Compositio Mathematica / Volume 145 / Issue 2 / March 2009
- Published online by Cambridge University Press:
- 01 March 2009, pp. 415-422
- Print publication:
- March 2009
-
- Article
-
- You have access
- Export citation
Réalisation de Hodge du polylogarithme d'un schéma abélien
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 8 / Issue 1 / January 2009
- Published online by Cambridge University Press:
- 20 November 2008, pp. 1-38
- Print publication:
- January 2009
-
- Article
- Export citation
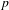
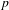




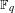
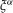

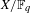

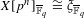
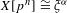
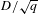
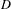


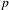

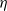
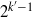
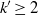
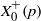
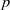
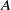
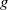
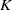
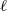
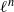
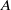
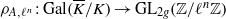
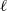
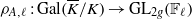
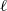
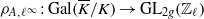
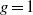
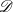
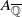 (the
(the 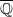 . Finally, we formulate and prove a variant of the Mordell–Lang conjecture for subvarieties of
. Finally, we formulate and prove a variant of the Mordell–Lang conjecture for subvarieties of 