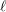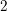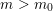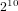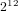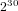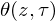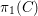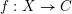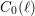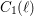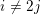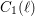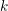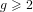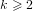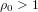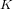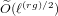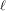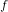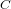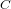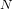Refine listing
Actions for selected content:
105 results in 14Kxx
Cycles in the de Rham cohomology of abelian varieties over number fields
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 4 / April 2018
- Published online by Cambridge University Press:
- 08 March 2018, pp. 850-882
- Print publication:
- April 2018
-
- Article
- Export citation
Corrigendum: Torsion points on abelian varieties of CM-type
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 3 / March 2018
- Published online by Cambridge University Press:
- 26 December 2017, p. 594
- Print publication:
- March 2018
-
- Article
-
- You have access
- HTML
- Export citation
A MODULI INTERPRETATION FOR THE NON-SPLIT CARTAN MODULAR CURVE
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 60 / Issue 2 / May 2018
- Published online by Cambridge University Press:
- 30 October 2017, pp. 411-434
- Print publication:
- May 2018
-
- Article
-
- You have access
- Export citation
Bad reduction of genus
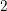 $2$ curves with CM jacobian varieties
$2$ curves with CM jacobian varieties
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 12 / December 2017
- Published online by Cambridge University Press:
- 11 September 2017, pp. 2534-2576
- Print publication:
- December 2017
-
- Article
- Export citation
On descending cohomology geometrically
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 7 / July 2017
- Published online by Cambridge University Press:
- 10 May 2017, pp. 1446-1478
- Print publication:
- July 2017
-
- Article
- Export citation
SOME NEW EXAMPLES OF SMASH-NILPOTENT ALGEBRAIC CYCLES
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 59 / Issue 3 / September 2017
- Published online by Cambridge University Press:
- 13 March 2017, pp. 623-634
- Print publication:
- September 2017
-
- Article
-
- You have access
- Export citation
Level structures on abelian varieties and Vojta’s conjecture
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 2 / February 2017
- Published online by Cambridge University Press:
- 06 February 2017, pp. 373-394
- Print publication:
- February 2017
-
- Article
- Export citation
Fast heuristic algorithms for computing relations in the class group of a quadratic order, with applications to isogeny evaluation
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue A / 2016
- Published online by Cambridge University Press:
- 26 August 2016, pp. 371-390
-
- Article
-
- You have access
- Export citation
Character theory approach to Sato–Tate groups
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue A / 2016
- Published online by Cambridge University Press:
- 26 August 2016, pp. 301-314
-
- Article
-
- You have access
- Export citation
Computing theta functions in quasi-linear time in genus two and above
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue A / 2016
- Published online by Cambridge University Press:
- 26 August 2016, pp. 163-177
-
- Article
-
- You have access
- Export citation
Gonality of abstract modular curves in positive characteristic
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 11 / November 2016
- Published online by Cambridge University Press:
- 29 July 2016, pp. 2405-2442
- Print publication:
- November 2016
-
- Article
- Export citation
The isotriviality of smooth families of canonically polarized manifolds over a special quasi-projective base
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 7 / July 2016
- Published online by Cambridge University Press:
- 26 April 2016, pp. 1421-1434
- Print publication:
- July 2016
-
- Article
- Export citation
Relative Manin–Mumford for Semi-Abelian Surfaces
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 59 / Issue 4 / November 2016
- Published online by Cambridge University Press:
- 18 January 2016, pp. 837-875
-
- Article
- Export citation
Logarithmic abelian varieties, Part IV: Proper models
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 219 / September 2015
- Published online by Cambridge University Press:
- 11 January 2016, pp. 9-63
- Print publication:
- September 2015
-
- Article
-
- You have access
- Export citation
Examples of CM curves of genus two defined over the reflex field
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 18 / Issue 1 / 2015
- Published online by Cambridge University Press:
- 01 August 2015, pp. 507-538
-
- Article
-
- You have access
- Export citation
Computing functions on Jacobians and their quotients
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 18 / Issue 1 / 2015
- Published online by Cambridge University Press:
- 01 August 2015, pp. 555-577
-
- Article
-
- You have access
- Export citation
ON THE NUMBER OF RATIONAL POINTS ON PRYM VARIETIES OVER FINITE FIELDS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 58 / Issue 1 / January 2016
- Published online by Cambridge University Press:
- 21 July 2015, pp. 55-68
- Print publication:
- January 2016
-
- Article
-
- You have access
- Export citation
Heuristics on pairing-friendly abelian varieties
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 18 / Issue 1 / 2015
- Published online by Cambridge University Press:
- 01 June 2015, pp. 419-443
-
- Article
-
- You have access
- Export citation
Computing separable isogenies in quasi-optimal time
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 18 / Issue 1 / 2015
- Published online by Cambridge University Press:
- 01 February 2015, pp. 198-216
-
- Article
-
- You have access
- Export citation
Genus-2 curves and Jacobians with a given number of points
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 18 / Issue 1 / 2015
- Published online by Cambridge University Press:
- 01 February 2015, pp. 170-197
-
- Article
-
- You have access
- Export citation