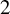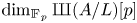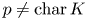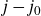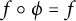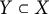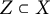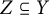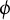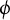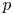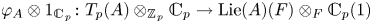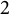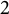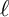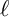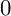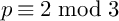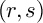Refine listing
Actions for selected content:
105 results in 14Kxx
Angehrn-Siu-Helmke’s method applied to abelian varieties
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 11 May 2023, e38
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Log p-divisible groups associated with log 1-motives
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 28 April 2023, pp. 946-983
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Effective characterization of quasi-abelian surfaces
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 02 February 2023, e7
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The Hodge bundle, the universal 0-section, and the log Chow ring of the moduli space of curves
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 2 / February 2023
- Published online by Cambridge University Press:
- 14 February 2023, pp. 306-354
- Print publication:
- February 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the distribution of rational points on ramified covers of abelian varieties
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 11 / November 2022
- Published online by Cambridge University Press:
- 07 December 2022, pp. 2109-2155
- Print publication:
- November 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The growth of Tate–Shafarevich groups in cyclic extensions
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 10 / October 2022
- Published online by Cambridge University Press:
- 04 November 2022, pp. 2014-2032
- Print publication:
- October 2022
-
- Article
- Export citation
Effective bounds on differences of singular moduli that are S-units
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 174 / Issue 2 / March 2023
- Published online by Cambridge University Press:
- 22 September 2022, pp. 415-450
- Print publication:
- March 2023
-
- Article
- Export citation
A conjecture strengthening the Zariski dense orbit problem for birational maps of dynamical degree one
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 07 July 2022, pp. 477-491
- Print publication:
- June 2023
-
- Article
- Export citation
On p-adic uniformization of abelian varieties with good reduction
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 7 / July 2022
- Published online by Cambridge University Press:
- 05 September 2022, pp. 1449-1476
- Print publication:
- July 2022
-
- Article
- Export citation
The logarithmic Picard group and its tropicalization
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 7 / July 2022
- Published online by Cambridge University Press:
- 09 September 2022, pp. 1477-1562
- Print publication:
- July 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Torsion codimension
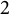 $2$ cycles on supersingular abelian varieties
$2$ cycles on supersingular abelian varieties
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 23 June 2022, pp. 458-466
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE BOUNDARY OF THE p-RANK
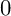 $0$ STRATUM OF THE MODULI SPACE OF CYCLIC COVERS OF THE PROJECTIVE LINE
$0$ STRATUM OF THE MODULI SPACE OF CYCLIC COVERS OF THE PROJECTIVE LINE
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 248 / December 2022
- Published online by Cambridge University Press:
- 30 May 2022, pp. 865-887
- Print publication:
- December 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Torsion points on isogenous abelian varieties
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 5 / May 2022
- Published online by Cambridge University Press:
- 20 July 2022, pp. 1020-1051
- Print publication:
- May 2022
-
- Article
- Export citation
APÉRY LIMITS FOR ELLIPTIC
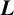 $\boldsymbol {L}$-VALUES
$\boldsymbol {L}$-VALUES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 2 / October 2022
- Published online by Cambridge University Press:
- 19 January 2022, pp. 273-279
- Print publication:
- October 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Faltings height and Néron–Tate height of a theta divisor
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 24 January 2022, pp. 1-32
- Print publication:
- January 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Corrigendum: Generic rank of Betti map and unlikely intersections
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 12 / December 2021
- Published online by Cambridge University Press:
- 05 January 2022, pp. 2747-2748
- Print publication:
- December 2021
-
- Article
-
- You have access
- HTML
- Export citation
Corrigendum: The affine part of the Picard scheme
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 10 / October 2021
- Published online by Cambridge University Press:
- 06 October 2021, pp. 2338-2340
- Print publication:
- October 2021
-
- Article
-
- You have access
- HTML
- Export citation
Singular units and isogenies between CM elliptic curves
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 5 / May 2021
- Published online by Cambridge University Press:
- 29 April 2021, pp. 1022-1035
- Print publication:
- May 2021
-
- Article
- Export citation
On certain Tannakian categories of integrable connections over Kähler manifolds
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 4 / August 2022
- Published online by Cambridge University Press:
- 21 April 2021, pp. 1034-1061
- Print publication:
- August 2022
-
- Article
- Export citation
Extending tamely ramified strict 1-motives into két log 1-motives
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 09 March 2021, e20
-
- Article
-
- You have access
- Open access
- Export citation