Refine listing
Actions for selected content:
1073 results in 05Cxx
Markov paths on the Poisson-Delaunay graph with applications to routeing in mobile networks
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 32 / Issue 1 / March 2000
- Published online by Cambridge University Press:
- 01 July 2016, pp. 1-18
- Print publication:
- March 2000
-
- Article
- Export citation
Phase transition in the random triangle model
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 36 / Issue 4 / December 1999
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1101-1115
- Print publication:
- December 1999
-
- Article
- Export citation
The central limit theorem for Euclidean minimal spanning trees II
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 31 / Issue 4 / December 1999
- Published online by Cambridge University Press:
- 01 July 2016, pp. 969-984
- Print publication:
- December 1999
-
- Article
- Export citation
Asymptotic properties of the connectivity number of random railways
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 31 / Issue 3 / September 1999
- Published online by Cambridge University Press:
- 01 July 2016, pp. 720-741
- Print publication:
- September 1999
-
- Article
- Export citation
On the size of a random sphere of influence graph
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 31 / Issue 3 / September 1999
- Published online by Cambridge University Press:
- 01 July 2016, pp. 596-609
- Print publication:
- September 1999
-
- Article
- Export citation
Epidemic processes on digraphs of random mappings
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 36 / Issue 3 / September 1999
- Published online by Cambridge University Press:
- 14 July 2016, pp. 780-798
- Print publication:
- September 1999
-
- Article
- Export citation
Asymptotics for geometric location problems over random samples
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 31 / Issue 3 / September 1999
- Published online by Cambridge University Press:
- 01 July 2016, pp. 632-642
- Print publication:
- September 1999
-
- Article
- Export citation
The random triangle model
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 36 / Issue 3 / September 1999
- Published online by Cambridge University Press:
- 14 July 2016, pp. 852-867
- Print publication:
- September 1999
-
- Article
- Export citation
Explicit sufficient invariants for an interacting particle system
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 35 / Issue 3 / September 1998
- Published online by Cambridge University Press:
- 14 July 2016, pp. 633-641
- Print publication:
- September 1998
-
- Article
- Export citation
Extremes for the minimal spanning tree on normally distributed points
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 30 / Issue 3 / September 1998
- Published online by Cambridge University Press:
- 01 July 2016, pp. 628-639
- Print publication:
- September 1998
-
- Article
- Export citation
Approximate upper bounds for the critical probability of oriented percolation in two dimensions based on rapidly mixing Markov chains
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 34 / Issue 4 / December 1997
- Published online by Cambridge University Press:
- 14 July 2016, pp. 859-867
- Print publication:
- December 1997
-
- Article
- Export citation
The Minimum Vertex Degree of a Graph on Uniform Points in [0, 1]d
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 29 / Issue 3 / September 1997
- Published online by Cambridge University Press:
- 01 July 2016, pp. 582-594
- Print publication:
- September 1997
-
- Article
- Export citation
The Maximum Vertex Degree of a Graph on Uniform Points in [0, 1]d
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 29 / Issue 3 / September 1997
- Published online by Cambridge University Press:
- 01 July 2016, pp. 567-581
- Print publication:
- September 1997
-
- Article
- Export citation
On the distribution of distances in recursive trees
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 33 / Issue 3 / September 1996
- Published online by Cambridge University Press:
- 14 July 2016, pp. 749-757
- Print publication:
- September 1996
-
- Article
- Export citation
Multivariate normal approximations by Stein's method and size bias couplings
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 33 / Issue 1 / March 1996
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1-17
- Print publication:
- March 1996
-
- Article
- Export citation
A regular endomorphism of a graph and its inverses
- Part of
-
- Journal:
- Mathematika / Volume 41 / Issue 1 / June 1994
- Published online by Cambridge University Press:
- 26 February 2010, pp. 189-198
- Print publication:
- June 1994
-
- Article
- Export citation
On the clique number of a random overlap graph
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 31 / Issue 2 / June 1994
- Published online by Cambridge University Press:
- 14 July 2016, pp. 582-588
- Print publication:
- June 1994
-
- Article
- Export citation
The Falling-Leaves Mosaic and its Equilibrium Properties
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 26 / Issue 1 / March 1994
- Published online by Cambridge University Press:
- 01 July 2016, pp. 54-62
- Print publication:
- March 1994
-
- Article
- Export citation
Factorial moments for random mappings by means of indicator variables
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 30 / Issue 1 / March 1993
- Published online by Cambridge University Press:
- 14 July 2016, pp. 167-174
- Print publication:
- March 1993
-
- Article
- Export citation
Giant components in three-parameter random directed graphs
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 24 / Issue 4 / December 1992
- Published online by Cambridge University Press:
- 01 July 2016, pp. 845-857
- Print publication:
- December 1992
-
- Article
- Export citation
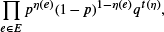
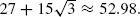 It is furthermore demonstrated that phase transition cannot occur unless
It is furthermore demonstrated that phase transition cannot occur unless 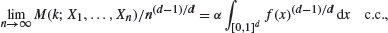
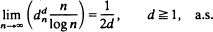
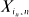 is asymptotically normal in several settings.
is asymptotically normal in several settings.