Refine listing
Actions for selected content:
1073 results in 05Cxx
Generating stationary random graphs on ℤ with prescribed independent, identically distributed degrees
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 38 / Issue 2 / June 2006
- Published online by Cambridge University Press:
- 01 July 2016, pp. 287-298
- Print publication:
- June 2006
-
- Article
-
- You have access
- Export citation
Limit distribution of distances in biased random tries
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 43 / Issue 2 / June 2006
- Published online by Cambridge University Press:
- 14 July 2016, pp. 377-390
- Print publication:
- June 2006
-
- Article
-
- You have access
- Export citation
On a conditionally Poissonian graph process
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 38 / Issue 1 / March 2006
- Published online by Cambridge University Press:
- 01 July 2016, pp. 59-75
- Print publication:
- March 2006
-
- Article
-
- You have access
- Export citation
Rooted edges of a minimal directed spanning tree on random points
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 38 / Issue 1 / March 2006
- Published online by Cambridge University Press:
- 01 July 2016, pp. 1-30
- Print publication:
- March 2006
-
- Article
-
- You have access
- Export citation
Quantitative Illumination of Convex Bodies and Vertex Degrees of Geometric Steiner Minimal Trees
- Part of
-
- Journal:
- Mathematika / Volume 52 / Issue 1-2 / December 2005
- Published online by Cambridge University Press:
- 21 December 2009, pp. 47-52
- Print publication:
- December 2005
-
- Article
- Export citation
Width of a scale-free tree
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 42 / Issue 3 / September 2005
- Published online by Cambridge University Press:
- 14 July 2016, pp. 839-850
- Print publication:
- September 2005
-
- Article
-
- You have access
- Export citation
Profiles of random trees: correlation and width of random recursive trees and binary search trees
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 37 / Issue 2 / June 2005
- Published online by Cambridge University Press:
- 01 July 2016, pp. 321-341
- Print publication:
- June 2005
-
- Article
-
- You have access
- Export citation
Connectivity of random k-nearest-neighbour graphs
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 37 / Issue 1 / March 2005
- Published online by Cambridge University Press:
- 01 July 2016, pp. 1-24
- Print publication:
- March 2005
-
- Article
-
- You have access
- Export citation
Random minimal directed spanning trees and Dickman-type distributions
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 36 / Issue 3 / September 2004
- Published online by Cambridge University Press:
- 01 July 2016, pp. 691-714
- Print publication:
- September 2004
-
- Article
- Export citation
A random hierarchical lattice: the series-parallel graph and its properties
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 36 / Issue 3 / September 2004
- Published online by Cambridge University Press:
- 01 July 2016, pp. 824-838
- Print publication:
- September 2004
-
- Article
- Export citation
On a random directed spanning tree
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 36 / Issue 1 / March 2004
- Published online by Cambridge University Press:
- 01 July 2016, pp. 19-42
- Print publication:
- March 2004
-
- Article
- Export citation
SIR epidemics on a Bernoulli random graph
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 40 / Issue 3 / September 2003
- Published online by Cambridge University Press:
- 14 July 2016, pp. 779-782
- Print publication:
- September 2003
-
- Article
- Export citation
Family trees of continuous-time birth-and-death processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 40 / Issue 4 / September 2003
- Published online by Cambridge University Press:
- 14 July 2016, pp. 980-994
- Print publication:
- September 2003
-
- Article
- Export citation
Coalescence times and F ST values in subdivided populations with symmetric structure
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 35 / Issue 3 / September 2003
- Published online by Cambridge University Press:
- 01 July 2016, pp. 665-690
- Print publication:
- September 2003
-
- Article
- Export citation
Optimal reward on a sparse tree with random edge weights
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 40 / Issue 4 / September 2003
- Published online by Cambridge University Press:
- 14 July 2016, pp. 926-945
- Print publication:
- September 2003
-
- Article
- Export citation
One-sided variations on interval trees
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 40 / Issue 3 / September 2003
- Published online by Cambridge University Press:
- 14 July 2016, pp. 654-670
- Print publication:
- September 2003
-
- Article
- Export citation
Compound random mappings
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 39 / Issue 4 / December 2002
- Published online by Cambridge University Press:
- 14 July 2016, pp. 712-729
- Print publication:
- December 2002
-
- Article
- Export citation
Focusing of the scan statistic and geometric clique number
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 34 / Issue 4 / December 2002
- Published online by Cambridge University Press:
- 01 July 2016, pp. 739-753
- Print publication:
- December 2002
-
- Article
- Export citation
Breakage and restoration in recursive trees
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 39 / Issue 2 / June 2002
- Published online by Cambridge University Press:
- 14 July 2016, pp. 383-390
- Print publication:
- June 2002
-
- Article
- Export citation
Sparse random matrices: spectral edge and statistics of rooted trees
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 33 / Issue 1 / March 2001
- Published online by Cambridge University Press:
- 01 July 2016, pp. 124-140
- Print publication:
- March 2001
-
- Article
- Export citation
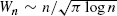 at the
at the