Refine listing
Actions for selected content:
115 results in 53Axx
ON THE INTEGRAL FORMULAS OF CROFTON AND HURWITZ RELATIVE TO THE VISUAL ANGLE OF A CONVEX SET
- Part of
-
- Journal:
- Mathematika / Volume 65 / Issue 4 / 2019
- Published online by Cambridge University Press:
- 21 May 2019, pp. 874-896
- Print publication:
- 2019
-
- Article
- Export citation
A Class of Parabolic Equations Driven by the Mean Curvature Flow
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 30 August 2018, pp. 135-163
-
- Article
- Export citation
THE ROSENTHAL–SZASZ INEQUALITY FOR NORMED PLANES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 29 August 2018, pp. 130-136
- Print publication:
- February 2019
-
- Article
-
- You have access
- Export citation
NEW COMPLEX ANALYTIC METHODS IN THE THEORY OF MINIMAL SURFACES: A SURVEY
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 106 / Issue 3 / June 2019
- Published online by Cambridge University Press:
- 23 August 2018, pp. 287-341
- Print publication:
- June 2019
-
- Article
-
- You have access
- Export citation
DYNAMIC ISOPERIMETRY ON GRAPHS AND WEIGHTED RIEMANNIAN MANIFOLDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 3 / December 2018
- Published online by Cambridge University Press:
- 15 August 2018, pp. 514-515
- Print publication:
- December 2018
-
- Article
-
- You have access
- Export citation
FOCAL SURFACES OF WAVE FRONTS IN THE EUCLIDEAN 3-SPACE
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 61 / Issue 2 / May 2019
- Published online by Cambridge University Press:
- 13 July 2018, pp. 425-440
- Print publication:
- May 2019
-
- Article
-
- You have access
- Export citation
ANY CYCLIC QUADRILATERAL CAN BE INSCRIBED IN ANY CLOSED CONVEX SMOOTH CURVE
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 6 / 2018
- Published online by Cambridge University Press:
- 31 May 2018, e7
-
- Article
-
- You have access
- Open access
- Export citation
TANGENT BUNDLES, MONOIDAL THEORIES AND WEIL ALGEBRAS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 1 / August 2018
- Published online by Cambridge University Press:
- 03 May 2018, pp. 175-176
- Print publication:
- August 2018
-
- Article
-
- You have access
- Export citation
Affine focal sets of codimension-2 submanifolds contained in hypersurfaces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 5 / October 2018
- Published online by Cambridge University Press:
- 22 April 2018, pp. 995-1016
- Print publication:
- October 2018
-
- Article
- Export citation
PROJECTIVE STRUCTURES AND
 $\unicode[STIX]{x1D70C}$-CONNECTIONS
$\unicode[STIX]{x1D70C}$-CONNECTIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 2 / March 2020
- Published online by Cambridge University Press:
- 22 March 2018, pp. 571-579
- Print publication:
- March 2020
-
- Article
- Export citation
A LOCAL UNIQUENESS THEOREM FOR MINIMIZERS OF PETTY’S CONJECTURED PROJECTION INEQUALITY
- Part of
-
- Journal:
- Mathematika / Volume 64 / Issue 1 / 2018
- Published online by Cambridge University Press:
- 24 January 2018, pp. 1-19
- Print publication:
- 2018
-
- Article
- Export citation
PARABOLIC CLASSICAL CURVATURE FLOWS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 104 / Issue 3 / June 2018
- Published online by Cambridge University Press:
- 30 October 2017, pp. 338-357
- Print publication:
- June 2018
-
- Article
-
- You have access
- Export citation
DISCRETE LINEAR WEINGARTEN SURFACES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 231 / September 2018
- Published online by Cambridge University Press:
- 04 September 2017, pp. 55-88
- Print publication:
- September 2018
-
- Article
-
- You have access
- HTML
- Export citation
ON THE EXISTENCE OF
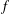 $f$ -MAXIMAL SPACELIKE HYPERSURFACES IN CERTAIN WEIGHTED MANIFOLDS
$f$ -MAXIMAL SPACELIKE HYPERSURFACES IN CERTAIN WEIGHTED MANIFOLDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 96 / Issue 2 / October 2017
- Published online by Cambridge University Press:
- 02 May 2017, pp. 317-325
- Print publication:
- October 2017
-
- Article
-
- You have access
- Export citation
Higher symmetries of powers of the Laplacian and rings of differential operators
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 4 / April 2017
- Published online by Cambridge University Press:
- 08 March 2017, pp. 678-716
- Print publication:
- April 2017
-
- Article
- Export citation
SUFFICIENT CONDITIONS FOR THE EXISTENCE OF LIMITING CARLEMAN WEIGHTS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 5 / 2017
- Published online by Cambridge University Press:
- 02 March 2017, e7
-
- Article
-
- You have access
- Open access
- Export citation
Bifurcation sets of families of reflections on surfaces in ℝ3
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 147 / Issue 2 / April 2017
- Published online by Cambridge University Press:
- 14 February 2017, pp. 337-352
- Print publication:
- April 2017
-
- Article
- Export citation
On Lorentzian surfaces in ℝ2,2
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 147 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 06 January 2017, pp. 61-88
- Print publication:
- February 2017
-
- Article
- Export citation
DIRECT EXPRESSION OF INCOMPATIBILITY IN CURVILINEAR SYSTEMS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 58 / Issue 1 / July 2016
- Published online by Cambridge University Press:
- 08 July 2016, pp. 33-50
-
- Article
-
- You have access
- Export citation
Separation of variables in equations of mean-curvature type
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 146 / Issue 5 / October 2016
- Published online by Cambridge University Press:
- 01 July 2016, pp. 1017-1035
- Print publication:
- October 2016
-
- Article
- Export citation
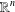
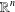
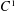
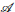 . We prove that the
. We prove that the 



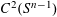
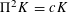
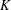

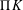
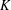
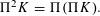
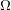
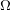
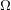
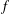
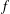
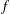
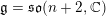
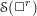

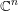
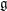
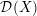
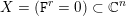
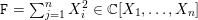
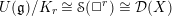
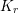

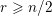
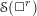
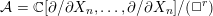
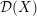
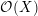
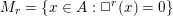
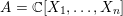
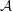
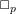
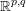
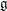
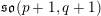
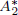 points’, which are not detected by the flat geometry of the surface. These
points’, which are not detected by the flat geometry of the surface. These 