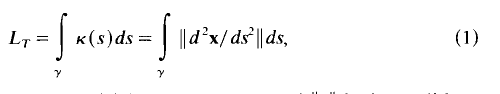Refine listing
Actions for selected content:
115 results in 53Axx
Delaunay ends of constant mean curvature surfaces
- Part of
-
- Journal:
- Compositio Mathematica / Volume 144 / Issue 1 / January 2008
- Published online by Cambridge University Press:
- 01 January 2008, pp. 186-220
- Print publication:
- January 2008
-
- Article
-
- You have access
- Export citation
Quasiregular self-mappings of manifolds and word hyperbolic groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 143 / Issue 6 / November 2007
- Published online by Cambridge University Press:
- 01 November 2007, pp. 1613-1622
- Print publication:
- November 2007
-
- Article
-
- You have access
- Export citation
The isoperimetric problem on some singular surfaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 78 / Issue 2 / April 2005
- Published online by Cambridge University Press:
- 09 April 2009, pp. 167-197
- Print publication:
- April 2005
-
- Article
-
- You have access
- Export citation
A uniqueness theorem for properly embedded minimal surfaces bounded by straight lines
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 69 / Issue 3 / December 2000
- Published online by Cambridge University Press:
- 09 April 2009, pp. 362-402
- Print publication:
- December 2000
-
- Article
-
- You have access
- Export citation
Self θ-congruent minimal surfaces in ℝ3
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 69 / Issue 2 / October 2000
- Published online by Cambridge University Press:
- 09 April 2009, pp. 229-244
- Print publication:
- October 2000
-
- Article
-
- You have access
- Export citation
Families of congruent curves and applications
- Part of
-
- Journal:
- Mathematika / Volume 46 / Issue 2 / December 1999
- Published online by Cambridge University Press:
- 26 February 2010, pp. 241-252
- Print publication:
- December 1999
-
- Article
- Export citation
Developable surfaces in Euclidean space
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 66 / Issue 3 / June 1999
- Published online by Cambridge University Press:
- 09 April 2009, pp. 388-402
- Print publication:
- June 1999
-
- Article
-
- You have access
- Export citation
Moduli space of branched superminimal immersions of a compact Riemann surface into S4
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 66 / Issue 1 / February 1999
- Published online by Cambridge University Press:
- 09 April 2009, pp. 32-50
- Print publication:
- February 1999
-
- Article
-
- You have access
- Export citation
The total curvature of a smooth closed curve in En is an upper bound to the total swing of its position vector
- Part of
-
- Journal:
- Mathematika / Volume 40 / Issue 1 / June 1993
- Published online by Cambridge University Press:
- 26 February 2010, pp. 148-151
- Print publication:
- June 1993
-
- Article
- Export citation
Hypersurfaces of En+1 Satisfying Δx = Ax + B
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 53 / Issue 3 / December 1992
- Published online by Cambridge University Press:
- 09 April 2009, pp. 377-384
- Print publication:
- December 1992
-
- Article
-
- You have access
- Export citation
On O. Bonnet III-isometry of surfaces in three dimensional Euclidean space
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 49 / Issue 1 / August 1990
- Published online by Cambridge University Press:
- 09 April 2009, pp. 90-110
- Print publication:
- August 1990
-
- Article
-
- You have access
- Export citation
Conformally Flat Riemannian Manifolds as Hypersurfaces of the Light Cone
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 32 / Issue 3 / 01 September 1989
- Published online by Cambridge University Press:
- 20 November 2018, pp. 281-285
- Print publication:
- 01 September 1989
-
- Article
-
- You have access
- Export citation
On concircular transformations in Riemannian spaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 40 / Issue 2 / April 1986
- Published online by Cambridge University Press:
- 09 April 2009, pp. 218-225
- Print publication:
- April 1986
-
- Article
-
- You have access
- Export citation
Conformally flat hypersurfaces of symmetric spaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 38 / Issue 2 / April 1985
- Published online by Cambridge University Press:
- 09 April 2009, pp. 207-213
- Print publication:
- April 1985
-
- Article
-
- You have access
- Export citation
Athwart immersions in Euclidean space
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 37 / Issue 2 / October 1984
- Published online by Cambridge University Press:
- 09 April 2009, pp. 282-286
- Print publication:
- October 1984
-
- Article
-
- You have access
- Export citation
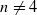 ), then every quasiregular mapping
), then every quasiregular mapping