We study the renormalized volume of asymptotically hyperbolic Einstein (AHE in short) manifolds $(M,g)$ when the conformal boundary $\unicode[STIX]{x2202}M$ has dimension $n$ even. Its definition depends on the choice of metric $h_{0}$ on $\unicode[STIX]{x2202}M$ in the conformal class at infinity determined by $g$, we denote it by $\text{Vol}_{R}(M,g;h_{0})$. We show that $\text{Vol}_{R}(M,g;\cdot )$ is a functional admitting a ‘Polyakov type’ formula in the conformal class $[h_{0}]$ and we describe the critical points as solutions of some non-linear equation $v_{n}(h_{0})=\text{constant}$, satisfied in particular by Einstein metrics. When $n=2$, choosing extremizers in the conformal class amounts to uniformizing the surface, while if $n=4$ this amounts to solving the $\unicode[STIX]{x1D70E}_{2}$-Yamabe problem. Next, we consider the variation of $\text{Vol}_{R}(M,\cdot ;\cdot )$ along a curve of AHE metrics $g^{t}$ with boundary metric $h_{0}^{t}$ and we use this to show that, provided conformal classes can be (locally) parametrized by metrics $h$ solving $v_{n}(h)=\text{constant}$ and $\text{Vol}(\unicode[STIX]{x2202}M,h)=1$, the set of ends of AHE manifolds (up to diffeomorphisms isotopic to the identity) can be viewed as a Lagrangian submanifold in the cotangent space to the space ${\mathcal{T}}(\unicode[STIX]{x2202}M)$ of conformal structures on $\unicode[STIX]{x2202}M$. We obtain, as a consequence, a higher-dimensional version of McMullen’s quasi-Fuchsian reciprocity. We finally show that conformal classes admitting negatively curved Einstein metrics are local minima for the renormalized volume for a warped product type filling.

We study the Minkowski symmetry set of a closed smooth curve γ in the Minkowski plane. We answer the following question, which is analogous to one concerning curves in the Euclidean plane that was treated by Giblin and O’Shea (1990): given a point p on γ, does there exist a bi-tangent pseudo-circle that is tangent to γ both at p and at some other point q on γ? The answer is yes, but as pseudo-circles with non-zero radii have two branches (connected components) it is possible to refine the above question to the following one: given a point p on γ, does there exist a branch of a pseudo-circle that is tangent to γ both at p and at some other point q on γ? This question is motivated by the earlier quest of Reeve and Tari (2014) to define the Minkowski Blum medial axis, a counterpart of the Blum medial axis of curves in the Euclidean plane.

The mobility of a Kähler metric is the dimension of the space of metrics with which it is c-projectively equivalent. The mobility is at least two if and only if the Kähler metric admits a nontrivial hamiltonian 2-form. After summarizing this relationship, we present necessary conditions for a Kähler metric to have mobility at least three: its curvature must have nontrivial nullity at every point. Using the local classification of Kähler metrics with hamiltonian 2-forms, we describe explicitly the Kähler metrics with mobility at least three and hence show that the nullity condition on the curvature is also sufficient, up to some degenerate exceptions. In an appendix, we explain how the classification may be related, generically, to the holonomy of a complex cone metric.

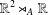In the ambient space of a semidirect product $\mathbb{R}^{2}\rtimes _{A}\mathbb{R}$, we consider a connected domain ${\rm\Omega}\subseteq \mathbb{R}^{2}\rtimes _{A}\{0\}$. Given a function $u:{\rm\Omega}\rightarrow \mathbb{R}$, its ${\it\pi}$-graph is $\text{graph}(u)=\{(x,y,u(x,y))\mid (x,y,0)\in {\rm\Omega}\}$. In this paper we study the partial differential equation that $u$ must satisfy so that $\text{graph}(u)$ has prescribed mean curvature $H$. Using techniques from quasilinear elliptic equations we prove that if a ${\it\pi}$-graph has a nonnegative mean curvature function, then it satisfies some uniform height estimates that depend on ${\rm\Omega}$ and on the supremum the function attains on the boundary of ${\rm\Omega}$. When $\text{trace}(A)>0$, we prove that the oscillation of a minimal graph, assuming the same constant value $n$ along the boundary, tends to zero when $n\rightarrow +\infty$ and goes to $+\infty$ if $n\rightarrow -\infty$. Furthermore, we use these estimates, allied with techniques from Killing graphs, to prove the existence of minimal ${\it\pi}$-graphs assuming the value zero along a piecewise smooth curve ${\it\gamma}$ with endpoints $p_{1},\,p_{2}$ and having as boundary ${\it\gamma}\cup (\{p_{1}\}\times [0,\,+\infty ))\cup (\{p_{2}\}\times [0,\,+\infty ))$.

We incorporate the new theory of equivariant moving frames for Lie pseudogroups into Vessiot’s method of group foliation of differential equations. The automorphic system is replaced by a set of reconstruction equations on the pseudogroup jets. The result is a completely algorithmic and symbolic procedure for finding both invariant and noninvariant solutions of differential equations admitting a symmetry group.

In this paper we study the Lorentzian surfaces with finite type Gauss map in the four-dimensional Minkowski space. First, we obtain the complete classification of minimal surfaces with pointwise 1-type Gauss map. Then, we get a classification of Lorentzian surfaces with nonzero constant mean curvature and of finite type Gauss map. We also give some explicit examples.

In this paper, we prove that, up to similarity, there are only two minimal hypersurfaces in $\mathbb{R}^{n+2}$ that are asymptotic to a Simons cone, i.e., the minimal cone over the minimal hypersurface $\sqrt{\frac{p}{n}}\mathbb{S}^{p}\times \sqrt{\frac{n-p}{n}}\mathbb{S}^{n-p}$ of $\mathbb{S}^{n+1}$ .

Extremal problems for quadrangles circuminscribed in a circular annulus with the Poncelet porism property are considered. Quadrangles with the maximal and the minimal perimeters are determined. Two conjectures end the paper.

We study properties of Sobolev-type metrics on the space of immersed plane curves. We show that the geodesic equation for Sobolev-type metrics with constant coefficients of order 2 and higher is globally well-posed for smooth initial data as well as for initial data in certain Sobolev spaces. Thus the space of closed plane curves equipped with such a metric is geodesically complete. We find lower bounds for the geodesic distance in terms of curvature and its derivatives.

We solve a randomized version of the following open question: is there a strictly convex, bounded curve $\gamma \subset { \mathbb{R} }^{2} $ such that the number of rational points on $\gamma $, with denominator $n$, approaches infinity with $n$? Although this natural problem appears to be out of reach using current methods, we consider a probabilistic analogue using a spatial Poisson process that simulates the refined rational lattice $(1/ d){ \mathbb{Z} }^{2} $, which we call ${M}_{d} $, for each natural number $d$. The main result here is that with probability $1$ there exists a strictly convex, bounded curve $\gamma $ such that $\vert \gamma \cap {M}_{d} \vert \rightarrow + \infty , $ as $d$ tends to infinity. The methods include the notion of a generalized affine length of a convex curve as defined by F. V. Petrov [Estimates for the number of rational points on convex curves and surfaces. Zap. Nauchn. Sem. S.-Peterburg. Otdel. Mat. Inst. Steklov. (POMI) 344 (2007), 174–189; Engl. transl. J. Math. Sci. 147(6) (2007), 7218–7226].

We examine the minimal magnitude of perturbations necessary to change the number $N$ of static equilibrium points of a convex solid $K$. We call the normalized volume of the minimally necessary truncation robustness and we seek shapes with maximal robustness for fixed values of $N$. While the upward robustness (referring to the increase of $N$) of smooth, homogeneous convex solids is known to be zero, little is known about their downward robustness. The difficulty of the latter problem is related to the coupling (via integrals) between the geometry of the hull $\mathrm{bd} \hspace{0.167em} K$ and the location of the center of gravity $G$. Here we first investigate two simpler, decoupled problems by examining truncations of $\mathrm{bd} \hspace{0.167em} K$ with $G$ fixed, and displacements of $G$ with $\mathrm{bd} \hspace{0.167em} K$ fixed, leading to the concept of external and internal robustness, respectively. In dimension 2, we find that for any fixed number $N= 2S$, the convex solids with both maximal external and maximal internal robustness are regular $S$-gons. Based on this result we conjecture that regular polygons have maximal downward robustness also in the original, coupled problem. We also show that in the decoupled problems, three-dimensional regular polyhedra have maximal internal robustness, however, only under additional constraints. Finally, we prove results for the full problem in the case of three-dimensional solids. These results appear to explain why monostatic pebbles (with either one stable or one unstable point of equilibrium) are found so rarely in nature.

It is shown that a minimal surface in ℍ2×ℝ is invariant under a one-parameter group of screw motions if and only if it lies in the associate family of helicoids. It is also shown that the conjugate surfaces of the parabolic and hyperbolic helicoids in ℍ2×ℝ are certain types of catenoids.

For a compact spacelike constant mean curvature surface with nonempty boundary in the three-dimensional Lorentz–Minkowski space, we introduce a rotation index of the lines of curvature at the boundary umbilical point, which was developed by Choe [‘Sufficient conditions for constant mean curvature surfaces to be round’, Math. Ann.323(1) (2002), 143–156]. 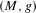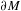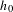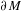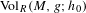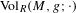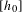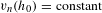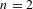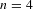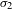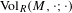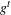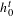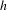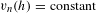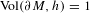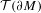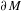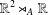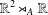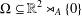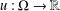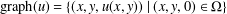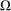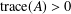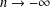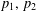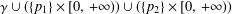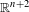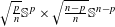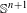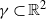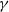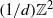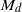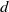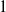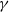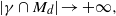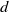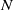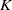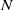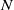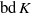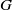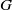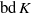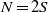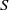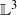Using the concept of the rotation index at the interior and boundary umbilical points and applying the Poincaré–Hopf index formula, we prove that a compact immersed spacelike disk type capillary surface with less than four vertices in a domain of bounded by (spacelike or timelike) totally umbilical surfaces is part of a (spacelike) plane or a hyperbolic plane. Moreover, we prove that the only immersed spacelike disk type capillary surface inside a de Sitter surface in is part of (spacelike) plane or a hyperbolic plane.

Given k ≥ 2, we construct a (2k − 2)-parameter family of properly embedded minimal surfaces in ℍ2 × ℝ invariant by a vertical translation T, called saddle towers, which have total intrinsic curvature 4π(1 − k), genus zero and 2k vertical Scherk-type ends in the quotient by T. Each of those examples is obtained from the conjugate graph of a Jenkins–Serrin graph over a convex polygonal domain with 2k edges of the same (finite) length. As limits of saddle towers, we obtain properly embedded minimal surfaces, called minimal k-noids, which are symmetric with respect to a horizontal slice (in fact they are vertical bi-graphs) and have total intrinsic curvature 4π(1 − k), genus zero and k vertical planar ends.

We detail a construction of totally symmetric surfaces of constant mean curvature 0≤H<1 in hyperbolic 3-space of sectional curvature −1 via the generalized Weierstrass type representation.

We prove that maximal annuli in 𝕃3 bounded by circles, straight lines or cone points in a pair of parallel spacelike planes are part of either a Lorentzian catenoid or a Lorentzian Riemann’s example. We show that under the same boundary condition, the same conclusion holds even when the maximal annuli have a planar end. Moreover, we extend Shiffman’s convexity result to maximal annuli; but by using Perron’s method we construct a maximal annulus with a planar end where a Shiffman-type result fails.

Using generalized position vector fields we obtain new upper bound estimates of the first nonzero eigenvalue of a kind of elliptic operator on closed submanifolds isometrically immersed in Riemannian manifolds of bounded sectional curvature. Applying these Reilly inequalities we improve a series of recent upper bound estimates of the first nonzero eigenvalue of the Lr operator on closed hypersurfaces in space forms.

This note contains a proof of the fact that a Jordan curve in ℝ2 with a continuous tangent line at each point admits a regular reparameterization. We extend the result both to more general curves in ℝn and to higher orders of differentiability.

We extend Penrose's peeling model for the asymptotic behaviour of solutions to the scalar wave equation at null infinity on asymptotically flat backgrounds, which is well understood for flat space-time, to Schwarzschild and the asymptotically simple space-times of Corvino–Schoen/Chrusciel–Delay. We combine conformal techniques and vector field methods: a naive adaptation of the ‘Morawetz vector field’ to a conformal rescaling of the Schwarzschild metric yields a complete scattering theory on Corvino–Schoen/Chrusciel–Delay space-times. A good classification of solutions that peel arises from the use of a null vector field that is transverse to null infinity to raise the regularity in the estimates. We obtain a new characterization of solutions admitting a peeling at a given order that is valid for both Schwarzschild and Minkowski space-times. On flat space-time, this allows larger classes of solutions than the characterizations used since Penrose's work. Our results establish the validity of the peeling model at all orders for the scalar wave equation on the Schwarzschild metric and on the corresponding Corvino–Schoen/Chrusciel–Delay space-times.

In the paper we prove that any closed finite type curve in the Euclidean space En(n≥2) lies in a null-space of a non-trivial polynomial P=P(x1,…,xn) of variables x1,…,xn, and thus lies on a surface of finite degree.