Refine listing
Actions for selected content:
490 results in 53Cxx
Consistency in systematic sampling
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 28 / Issue 4 / December 1996
- Published online by Cambridge University Press:
- 01 July 2016, pp. 982-992
- Print publication:
- December 1996
-
- Article
- Export citation
When can one domain enclose another in
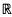 3?
3?
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 59 / Issue 2 / October 1995
- Published online by Cambridge University Press:
- 09 April 2009, pp. 266-272
- Print publication:
- October 1995
-
- Article
-
- You have access
- Export citation
A comparison theorem for the first Dirichlet eigenvalue of a domain in a Kaehler submanifold
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 56 / Issue 2 / April 1994
- Published online by Cambridge University Press:
- 09 April 2009, pp. 267-277
- Print publication:
- April 1994
-
- Article
-
- You have access
- Export citation
Unbiased Stereological Estimation of d-Dimensional Volume in ℝn from an Isotropic Random Slice Through a Fixed Point
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 26 / Issue 1 / March 1994
- Published online by Cambridge University Press:
- 01 July 2016, pp. 1-12
- Print publication:
- March 1994
-
- Article
- Export citation
The minimal volume of the plane
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 55 / Issue 1 / August 1993
- Published online by Cambridge University Press:
- 09 April 2009, pp. 23-40
- Print publication:
- August 1993
-
- Article
-
- You have access
- Export citation
Hypersurfaces of En+1 Satisfying Δx = Ax + B
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 53 / Issue 3 / December 1992
- Published online by Cambridge University Press:
- 09 April 2009, pp. 377-384
- Print publication:
- December 1992
-
- Article
-
- You have access
- Export citation
Contact structures on 1-connected 5-manifolds
- Part of
-
- Journal:
- Mathematika / Volume 38 / Issue 2 / December 1991
- Published online by Cambridge University Press:
- 26 February 2010, pp. 303-311
- Print publication:
- December 1991
-
- Article
- Export citation
Harmonic morphisms and conformal foliations by geodesics of three-dimensional space forms
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 51 / Issue 1 / August 1991
- Published online by Cambridge University Press:
- 09 April 2009, pp. 118-153
- Print publication:
- August 1991
-
- Article
-
- You have access
- Export citation
On the consecutive eigenvalues of the Laplacian of a compact minimal submanifold in a sphere
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 50 / Issue 3 / June 1991
- Published online by Cambridge University Press:
- 09 April 2009, pp. 409-416
- Print publication:
- June 1991
-
- Article
-
- You have access
- Export citation
Critical associated metrics on contact manifolds III
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 50 / Issue 2 / April 1991
- Published online by Cambridge University Press:
- 09 April 2009, pp. 189-196
- Print publication:
- April 1991
-
- Article
-
- You have access
- Export citation
Conformally Flat Riemannian Manifolds as Hypersurfaces of the Light Cone
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 32 / Issue 3 / 01 September 1989
- Published online by Cambridge University Press:
- 20 November 2018, pp. 281-285
- Print publication:
- 01 September 1989
-
- Article
-
- You have access
- Export citation
A note on real hypersurfaces of a complex projective space
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 47 / Issue 1 / August 1989
- Published online by Cambridge University Press:
- 09 April 2009, pp. 108-113
- Print publication:
- August 1989
-
- Article
-
- You have access
- Export citation
Complete hypersurfaces in cylinders
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 46 / Issue 2 / April 1989
- Published online by Cambridge University Press:
- 09 April 2009, pp. 313-318
- Print publication:
- April 1989
-
- Article
-
- You have access
- Export citation
Integral inequalities for ovaloids in Euclidean space
- Part of
-
- Journal:
- Mathematika / Volume 34 / Issue 1 / June 1987
- Published online by Cambridge University Press:
- 26 February 2010, pp. 77-81
- Print publication:
- June 1987
-
- Article
- Export citation
Critical associated metrics on contact manifolds. II
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 41 / Issue 3 / December 1986
- Published online by Cambridge University Press:
- 09 April 2009, pp. 404-410
- Print publication:
- December 1986
-
- Article
-
- You have access
- Export citation
Conformally flat hypersurfaces of symmetric spaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 38 / Issue 2 / April 1985
- Published online by Cambridge University Press:
- 09 April 2009, pp. 207-213
- Print publication:
- April 1985
-
- Article
-
- You have access
- Export citation
On the reconstruction of a star-shaped body from its “half-volumes”
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 37 / Issue 2 / October 1984
- Published online by Cambridge University Press:
- 09 April 2009, pp. 243-257
- Print publication:
- October 1984
-
- Article
-
- You have access
- Export citation
Critical associated metrics on contact manifolds
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 37 / Issue 1 / August 1984
- Published online by Cambridge University Press:
- 09 April 2009, pp. 82-88
- Print publication:
- August 1984
-
- Article
-
- You have access
- Export citation
Generalized Minkowski formulae for compact submanifolds of a Riemannian manifold
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 36 / Issue 3 / June 1984
- Published online by Cambridge University Press:
- 09 April 2009, pp. 378-388
- Print publication:
- June 1984
-
- Article
-
- You have access
- Export citation
Submanifolds and the length of the second fundamental tensor
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 34 / Issue 1 / February 1983
- Published online by Cambridge University Press:
- 09 April 2009, pp. 1-6
- Print publication:
- February 1983
-
- Article
-
- You have access
- Export citation