We prove that maximal annuli in 𝕃3 bounded by circles, straight lines or cone points in a pair of parallel spacelike planes are part of either a Lorentzian catenoid or a Lorentzian Riemann’s example. We show that under the same boundary condition, the same conclusion holds even when the maximal annuli have a planar end. Moreover, we extend Shiffman’s convexity result to maximal annuli; but by using Perron’s method we construct a maximal annulus with a planar end where a Shiffman-type result fails.

In this article we study the Kähler–Ricci flow, the corresponding parabolic Monge–Ampère equation and complete non-compact Kähler–Ricci flat manifolds. Our main result states that if (M,g) is sufficiently close to being Kähler–Ricci flat in a suitable sense, then the Kähler–Ricci flow has a long time smooth solution g(t) converging smoothly uniformly on compact sets to a complete Kähler–Ricci flat metric on M. The main step is to obtain a uniform C0-estimate for the corresponding parabolic Monge–Ampère equation. Our results on this can be viewed as parabolic versions of the main results of Tian and Yau [Complete Kähler manifolds with zero Ricci curvature. II, Invent. Math. 106 (1990), 27–60] on the elliptic Monge–Ampère equation.

We prove that Alexandrov spaces of non-negative curvature have Markov type 2 in the sense of Ball. As a corollary, any Lipschitz continuous map from a subset of an Alexandrov space of non-negative curvature into a 2-uniformly convex Banach space can be extended to a Lipschitz continuous map on the entire space.

It is known that there are no real hypersurfaces with parallel structure Jacobi operators in a nonflat complex space form. In this paper, we classify real hypersurfaces in a nonflat complex space form whose structure Jacobi operator is cyclic-parallel.

Using generalized position vector fields we obtain new upper bound estimates of the first nonzero eigenvalue of a kind of elliptic operator on closed submanifolds isometrically immersed in Riemannian manifolds of bounded sectional curvature. Applying these Reilly inequalities we improve a series of recent upper bound estimates of the first nonzero eigenvalue of the Lr operator on closed hypersurfaces in space forms.

In this paper we get different characterizations of the spherical strictly pseudoconvex CR manifolds admitting a CR-symmetric Webster metric by means of the Tanaka–Webster connection and of the Riemannian curvature tensor. As a consequence we obtain the classification of the simply connected, spherical symmetric pseudo-Hermitian manifolds.

We prove that in any compact symmetric space, G/K, there is a dense set of a1,a2∈G such that if μj=mK*δaj*mk is the K-bi-invariant measure supported on KajK, then μ1*μ2 is absolutely continuous with respect to Haar measure on G. Moreover, the product of double cosets, Ka1Ka2K, has nonempty interior in G.

We give conditions which imply that a complete noncompact manifold with quadratic curvature decay has finite topological type. In particular, we find links between the topology of a manifold with quadratic curvature decay and some properties of the asymptotic cones of such a manifold.

In this paper we consider the dynamical system involved by the Ricci operator on the space of Kähler metrics of a Fano manifold. Nadel has defined an iteration scheme given by the Ricci operator and asked whether it has some non-trivial periodic points. First, we prove that no such periodic points can exist. We define the inverse of the Ricci operator and consider the dynamical behaviour of its iterates for a Fano Kähler–Einstein manifold. Then we define a finite-dimensional procedure to give an approximation of Kähler–Einstein metrics using this iterative procedure and apply it on ℂℙ2 blown up in three points.

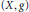
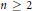
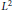
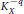
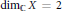
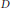
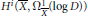
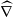By using the pseudo-Hermitian connection (or Tanaka–Webster connection) , we construct the parametric equations of Legendre pseudo-Hermitian circles (whose -geodesic curvature 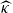is constant and 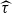-geodesic torsion is zero) in S3. In fact, it is realized as a Legendre curve satisfying the -Jacobi equation for the -geodesic vector field along it.

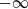Let N be a complete Riemannian manifold isometrically immersed into a Hadamard manifold M. We show that the immersion cannot be bounded if the mean curvature of the immersed manifold is small compared with the curvature of M and the Laplacian of the distance function on N grows at most linearly. The latter condition is satisfied if the Ricci curvature of N does not approach too fast. The main tool in the proof is a modification of Yau’s maximum principle.

In this paper we give a nonexistence theorem for real hypersurfaces in complex two-plane Grassmannians G2(ℂm+2) with anti-commuting shape operator.

We discuss the isoperimetric problem in planes with density. In particular, we examine planes with generalized curvature zero. We solve the isoperimetric problem on the plane with density ex, as well as on the plane with density rp for p<0. The Appendix provides a proof by Robert Bryant that the Gauss plane has a unique closed geodesic.

In thispaper we find many families in the product space ℍ2×ℝ of complete embedded, simply connected, minimal and surfaces with constant mean curvature H such that |H|≤1/2. We study complete surfaces invariant either by parabolic or by hyperbolic screw motions. We study the notion of isometric associate immersions. We exhibit an explicit formula for a Scherk-type minimal surface. We give a one-parameter family of entire vertical graphs of mean curvature 1/2. We prove a generalized Bour lemma that can be applied to ℍ2×ℝ,𝕊2×ℝ and to Heisenberg’s space to produce a family of screw motion surfaces isometric to a given one.

We derive upper Gaussian bounds for the heat kernel on complete, noncompact locally symmetric spaces M=Γ∖X with nonpositive curvature. Our bounds contain the Poincaré series of the discrete group Γ and therefore we also provide upper bounds for this series.

Given a Lie n-algebra, we provide an explicit construction of its integrating Lie n-group. This extends work done by Getzler in the case of nilpotent -algebras. When applied to an ordinary Lie algebra, our construction yields the simplicial classifying space of the corresponding simply connected Lie group. In the case of the string Lie 2-algebra of Baez and Crans, we obtain the simplicial nerve of their model of the string group.

We describe a contact metric manifold whose Reeb vector field belongs to the (κ,μ)-nullity distribution as a bi-Legendrian manifold and we study its canonical bi-Legendrian structure. Then we characterize contact metric (κ,μ)-spaces in terms of a canonical connection which can be naturally defined on them.

The equivalence between contact and Pansu differentiable maps on Carnot groups is established within the class of maps that are C1 with respect to the ambient Euclidean structure.

The problem of finding geodesics that avoid certain obstacles in negatively curved manifolds has been studied in different situations. In this note we give a generalization of the unclouding theorem of J. Parkkonen and F. Paulin: there is a constant s0=1.534 such that for any Hadamard manifold M with curvature ≤−1 and for any family of disjoint balls or horoballs {Ca}a∈A and for any point p∈M−⋃ a∈ACa if we shrink these balls uniformly by s0 one can always find a geodesic ray emanating from p that avoids the shrunk balls. It will be shown that in the theorem above one can replace the balls by arbitrary convex sets.

We construct a Kähler structure (which we call a generalised Kähler cone) on an open subset of the cone of a strongly pseudo-convex CR manifold endowed with a one-parameter family of compatible Sasaki structures. We determine those generalised Kähler cones which are Bochner-flat and we study their local geometry. We prove that any Bochner-flat Kähler manifold of complex dimension bigger than two is locally isomorphic to a generalised Kähler cone.