Refine listing
Actions for selected content:
490 results in 53Cxx
BIHARMONIC SUBMANIFOLDS IN NONFLAT LORENTZ 3-SPACE FORMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 85 / Issue 3 / June 2012
- Published online by Cambridge University Press:
- 30 November 2011, pp. 422-432
- Print publication:
- June 2012
-
- Article
-
- You have access
- Export citation
Kähler groups, real hyperbolic spaces and the Cremona group. With an appendix by Serge Cantat
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 1 / January 2012
- Published online by Cambridge University Press:
- 30 November 2011, pp. 153-184
- Print publication:
- January 2012
-
- Article
-
- You have access
- Export citation
H-CONTACT UNIT TANGENT SPHERE BUNDLES OF FOUR-DIMENSIONAL RIEMANNIAN MANIFOLDS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 91 / Issue 2 / October 2011
- Published online by Cambridge University Press:
- 21 September 2011, pp. 243-256
- Print publication:
- October 2011
-
- Article
-
- You have access
- Export citation
Existence and non-uniqueness of constant scalar curvature toric Sasaki metrics
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 5 / September 2011
- Published online by Cambridge University Press:
- 27 July 2011, pp. 1613-1634
- Print publication:
- September 2011
-
- Article
-
- You have access
- Export citation
ON MINIMAL SURFACES SATISFYING THE OMORI–YAU PRINCIPLE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 84 / Issue 1 / August 2011
- Published online by Cambridge University Press:
- 16 June 2011, pp. 33-39
- Print publication:
- August 2011
-
- Article
-
- You have access
- Export citation
Location of geodesics and isoperimetric inequalities in Denjoy domains
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 55 / Issue 1 / February 2012
- Published online by Cambridge University Press:
- 15 June 2011, pp. 245-269
-
- Article
-
- You have access
- Export citation
INVARIANT EINSTEIN METRICS ON GENERALIZED FLAG MANIFOLDS WITH TWO ISOTROPY SUMMANDS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 90 / Issue 2 / April 2011
- Published online by Cambridge University Press:
- 19 July 2011, pp. 237-251
- Print publication:
- April 2011
-
- Article
-
- You have access
- Export citation
A CHARACTERIZATION OF SPECIAL SUBVARIETIES
- Part of
-
- Journal:
- Mathematika / Volume 57 / Issue 2 / July 2011
- Published online by Cambridge University Press:
- 07 March 2011, pp. 263-273
- Print publication:
- July 2011
-
- Article
- Export citation
CONVOLUTION OF ORBITAL MEASURES IN SYMMETRIC SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 83 / Issue 3 / June 2011
- Published online by Cambridge University Press:
- 09 February 2011, pp. 470-485
- Print publication:
- June 2011
-
- Article
-
- You have access
- Export citation
ON THE STABILITY OF STATIONARY LINE AND GRIM REAPER IN PLANAR CURVATURE FLOW
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 83 / Issue 2 / April 2011
- Published online by Cambridge University Press:
- 07 February 2011, pp. 177-188
- Print publication:
- April 2011
-
- Article
-
- You have access
- Export citation
A NOTE ON BUNDLE GERBES AND INFINITE-DIMENSIONALITY
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 90 / Issue 1 / February 2011
- Published online by Cambridge University Press:
- 22 March 2011, pp. 81-92
- Print publication:
- February 2011
-
- Article
-
- You have access
- Export citation
A LOOP SPACE FORMULATION FOR GEOMETRIC LIFTING PROBLEMS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 90 / Issue 1 / February 2011
- Published online by Cambridge University Press:
- 09 June 2011, pp. 129-144
- Print publication:
- February 2011
-
- Article
-
- You have access
- Export citation
FOURTH ORDER GEOMETRIC EVOLUTION EQUATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 82 / Issue 3 / December 2010
- Published online by Cambridge University Press:
- 18 November 2010, pp. 523-524
- Print publication:
- December 2010
-
- Article
-
- You have access
- Export citation
Closed Einstein–Weyl structures on compact Sasakian and cosymplectic manifolds
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 54 / Issue 1 / February 2011
- Published online by Cambridge University Press:
- 11 November 2010, pp. 149-160
-
- Article
-
- You have access
- Export citation
Notes on contact Ricci solitons
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 54 / Issue 1 / February 2011
- Published online by Cambridge University Press:
- 28 October 2010, pp. 47-53
-
- Article
-
- You have access
- Export citation
The Calabi–Yau equation on the Kodaira–Thurston manifold
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 10 / Issue 2 / April 2011
- Published online by Cambridge University Press:
- 24 September 2010, pp. 437-447
- Print publication:
- April 2011
-
- Article
- Export citation
Greatest lower bounds on the Ricci curvature of Fano manifolds
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 1 / January 2011
- Published online by Cambridge University Press:
- 17 August 2010, pp. 319-331
- Print publication:
- January 2011
-
- Article
-
- You have access
- Export citation
Gray identities, canonical connection and integrability
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 53 / Issue 3 / October 2010
- Published online by Cambridge University Press:
- 12 August 2010, pp. 657-674
-
- Article
-
- You have access
- Export citation
On the quasi-asymptotically locally Euclidean geometry of Nakajima's metric
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 10 / Issue 1 / January 2011
- Published online by Cambridge University Press:
- 29 June 2010, pp. 119-147
- Print publication:
- January 2011
-
- Article
- Export citation
HOMOGENEOUS AND H-CONTACT UNIT TANGENT SPHERE BUNDLES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 88 / Issue 3 / June 2010
- Published online by Cambridge University Press:
- 12 May 2010, pp. 323-337
- Print publication:
- June 2010
-
- Article
-
- You have access
- Export citation
 is a Riemannian
is a Riemannian 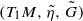 is
is 