Refine listing
Actions for selected content:
490 results in 53Cxx
A Decomposition Theorem for Immersions of Product Manifolds
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 59 / Issue 1 / February 2016
- Published online by Cambridge University Press:
- 17 April 2015, pp. 247-269
-
- Article
- Export citation
THE MINIMAL
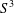 $S^{3}$ WITH CONSTANT SECTIONAL CURVATURE IN
$S^{3}$ WITH CONSTANT SECTIONAL CURVATURE IN 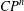 $\mathit{CP}^{n}$
$\mathit{CP}^{n}$
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 99 / Issue 1 / August 2015
- Published online by Cambridge University Press:
- 18 February 2015, pp. 63-75
- Print publication:
- August 2015
-
- Article
-
- You have access
- Export citation
THE METRIC DIMENSION OF METRIC MANIFOLDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 91 / Issue 3 / June 2015
- Published online by Cambridge University Press:
- 11 February 2015, pp. 508-513
- Print publication:
- June 2015
-
- Article
-
- You have access
- Export citation
KILLING FRAMES AND S-CURVATURE OF HOMOGENEOUS FINSLER SPACES*
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 57 / Issue 2 / May 2015
- Published online by Cambridge University Press:
- 22 December 2014, pp. 457-464
- Print publication:
- May 2015
-
- Article
-
- You have access
- Export citation
ON BI-HARMONIC HYPERSURFACES IN EUCLIDEAN SPACE OF ARBITRARY DIMENSION
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 57 / Issue 3 / September 2015
- Published online by Cambridge University Press:
- 18 December 2014, pp. 633-642
- Print publication:
- September 2015
-
- Article
-
- You have access
- Export citation
QUASI-EINSTEIN CONTACT METRIC MANIFOLDS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 57 / Issue 3 / September 2015
- Published online by Cambridge University Press:
- 18 December 2014, pp. 569-577
- Print publication:
- September 2015
-
- Article
-
- You have access
- Export citation
CHARACTERIZATIONS OF RICCI FLAT METRICS AND LAGRANGIAN SUBMANIFOLDS IN TERMS OF THE VARIATIONAL PROBLEM
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 57 / Issue 3 / September 2015
- Published online by Cambridge University Press:
- 17 December 2014, pp. 643-651
- Print publication:
- September 2015
-
- Article
-
- You have access
- Export citation
LINEAR WEINGARTEN HYPERSURFACES WITH BOUNDED MEAN CURVATURE IN THE HYPERBOLIC SPACE
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 57 / Issue 3 / September 2015
- Published online by Cambridge University Press:
- 17 December 2014, pp. 653-663
- Print publication:
- September 2015
-
- Article
-
- You have access
- Export citation
ON DIFFERENTIAL CHARACTERISTIC CLASSES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 99 / Issue 1 / August 2015
- Published online by Cambridge University Press:
- 04 December 2014, pp. 30-47
- Print publication:
- August 2015
-
- Article
-
- You have access
- Export citation
Statistics for Poisson Models of Overlapping Spheres
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 46 / Issue 4 / December 2014
- Published online by Cambridge University Press:
- 22 February 2016, pp. 937-962
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
Size distributions in random triangles
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 51 / Issue A / December 2014
- Published online by Cambridge University Press:
- 30 March 2016, pp. 283-295
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
CONVOLUTION OF ORBITAL MEASURES ON SYMMETRIC SPACES OF TYPE
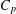 $C_{p}$ AND
$C_{p}$ AND 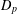 $D_{p}$
$D_{p}$
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 98 / Issue 2 / April 2015
- Published online by Cambridge University Press:
- 11 November 2014, pp. 232-256
- Print publication:
- April 2015
-
- Article
-
- You have access
- Export citation
A Sharp Height Estimate for Compact Hypersurfaces with Constant k-Mean Curvature in Warped Product Spaces
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 58 / Issue 2 / June 2015
- Published online by Cambridge University Press:
- 27 October 2014, pp. 403-419
-
- Article
-
- You have access
- Export citation
A NOTE ON THE MORSE–NOVIKOV COHOMOLOGY OF BLOW-UPS OF LOCALLY CONFORMAL KÄHLER MANIFOLDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 91 / Issue 1 / February 2015
- Published online by Cambridge University Press:
- 14 October 2014, pp. 155-166
- Print publication:
- February 2015
-
- Article
-
- You have access
- Export citation
A NEW RESULT ABOUT ALMOST UMBILICAL HYPERSURFACES OF REAL SPACE FORMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 91 / Issue 1 / February 2015
- Published online by Cambridge University Press:
- 14 October 2014, pp. 145-154
- Print publication:
- February 2015
-
- Article
-
- You have access
- Export citation
REMARKS ON BIANCHI SUMS AND PONTRJAGIN CLASSES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 97 / Issue 3 / December 2014
- Published online by Cambridge University Press:
- 24 September 2014, pp. 365-382
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
WARPED PRODUCTS IN RIEMANNIAN MANIFOLDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 90 / Issue 3 / December 2014
- Published online by Cambridge University Press:
- 09 September 2014, pp. 510-520
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
Trihyperkähler reduction and instanton bundles on
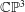 $\mathbb{C}\mathbb{P}^{3}$
$\mathbb{C}\mathbb{P}^{3}$
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 11 / November 2014
- Published online by Cambridge University Press:
- 27 August 2014, pp. 1836-1868
- Print publication:
- November 2014
-
- Article
- Export citation
Reduction of Homogeneous Riemannian Structures
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 58 / Issue 1 / February 2015
- Published online by Cambridge University Press:
- 18 July 2014, pp. 81-106
-
- Article
-
- You have access
- Export citation
FINSLER METRIZABLE ISOTROPIC SPRAYS AND HILBERT’S FOURTH PROBLEM
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 97 / Issue 1 / August 2014
- Published online by Cambridge University Press:
- 20 May 2014, pp. 27-47
- Print publication:
- August 2014
-
- Article
-
- You have access
- Export citation
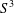
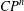

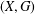
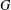
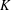
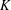
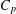
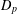
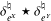
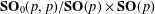
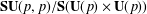
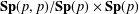
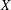
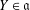
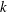
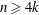
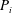
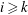
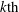
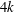
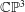
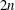
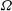
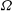
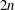


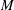
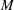


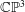
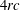

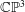
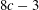
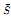 . The situation when
. The situation when 