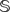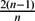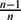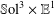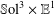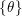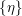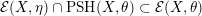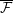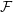Refine listing
Actions for selected content:
490 results in 53Cxx
Eigenvalue Ratios of Non-Negatively Curved Graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 27 / Issue 5 / September 2018
- Published online by Cambridge University Press:
- 23 May 2018, pp. 829-850
-
- Article
- Export citation
Cohomology of Flat Principal Bundles
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 3 / August 2018
- Published online by Cambridge University Press:
- 22 May 2018, pp. 869-877
-
- Article
- Export citation
From ALE to ALF gravitational instantons
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 6 / June 2018
- Published online by Cambridge University Press:
- 03 May 2018, pp. 1159-1221
- Print publication:
- June 2018
-
- Article
- Export citation
CONVERGENCE OF MANN’S ALTERNATING PROJECTIONS IN CAT(
 $\unicode[STIX]{x1D705}$ ) SPACES
$\unicode[STIX]{x1D705}$ ) SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 1 / August 2018
- Published online by Cambridge University Press:
- 03 May 2018, pp. 134-143
- Print publication:
- August 2018
-
- Article
-
- You have access
- Export citation
Deforming an є-close-to-hyperbolic metric to a hyperbolic metric
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 3 / June 2018
- Published online by Cambridge University Press:
- 18 April 2018, pp. 629-641
- Print publication:
- June 2018
-
- Article
- Export citation
A COMPACTNESS THEOREM FOR SURFACES WITH BOUNDED INTEGRAL CURVATURE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 2 / March 2020
- Published online by Cambridge University Press:
- 10 April 2018, pp. 597-645
- Print publication:
- March 2020
-
- Article
- Export citation
PROJECTIVE STRUCTURES AND
 $\unicode[STIX]{x1D70C}$-CONNECTIONS
$\unicode[STIX]{x1D70C}$-CONNECTIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 2 / March 2020
- Published online by Cambridge University Press:
- 22 March 2018, pp. 571-579
- Print publication:
- March 2020
-
- Article
- Export citation
Non-Negative Curvature, Elliptic Genus and Unbounded Pontryagin Numbers
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 2 / May 2018
- Published online by Cambridge University Press:
- 26 February 2018, pp. 449-456
-
- Article
- Export citation
The structure of the Ricci tensor on locally homogeneous Lorentzian gradient Ricci solitons
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 3 / June 2018
- Published online by Cambridge University Press:
- 22 February 2018, pp. 461-482
- Print publication:
- June 2018
-
- Article
- Export citation
VANISHING THEOREMS FOR HYPERSURFACES IN THE UNIT SPHERE
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 60 / Issue 3 / September 2018
- Published online by Cambridge University Press:
- 28 January 2018, pp. 661-671
- Print publication:
- September 2018
-
- Article
-
- You have access
- Export citation
Displacement convexity for the entropy in semi-discrete non-linear Fokker–Planck equations
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 30 / Issue 6 / December 2019
- Published online by Cambridge University Press:
- 10 January 2018, pp. 1103-1122
-
- Article
-
- You have access
- Open access
- Export citation
CLASSIFICATION OF SPIN STRUCTURES ON FOUR-DIMENSIONAL ALMOST-FLAT MANIFOLDS
- Part of
-
- Journal:
- Mathematika / Volume 64 / Issue 1 / 2018
- Published online by Cambridge University Press:
- 14 February 2018, pp. 253-266
- Print publication:
- 2018
-
- Article
- Export citation
Evolution of non-simple closed curves in the area-preserving curvature flow
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 3 / June 2018
- Published online by Cambridge University Press:
- 28 December 2017, pp. 659-668
- Print publication:
- June 2018
-
- Article
- Export citation
SPACE OF RICCI FLOWS (II)—PART A:MODULI OF SINGULAR CALABI–YAU SPACES
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 5 / 2017
- Published online by Cambridge University Press:
- 28 December 2017, e32
-
- Article
-
- You have access
- Open access
- Export citation
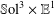 $\mathbb{S}\text{ol}^{3}\times \mathbb{E}^{1}$ -MANIFOLDS
$\mathbb{S}\text{ol}^{3}\times \mathbb{E}^{1}$ -MANIFOLDS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 105 / Issue 1 / August 2018
- Published online by Cambridge University Press:
- 04 December 2017, pp. 46-56
- Print publication:
- August 2018
-
- Article
-
- You have access
- Export citation
On the singularity type of full mass currents in big cohomology classes
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 2 / February 2018
- Published online by Cambridge University Press:
- 09 November 2017, pp. 380-409
- Print publication:
- February 2018
-
- Article
- Export citation
ON HARMONIC AND PSEUDOHARMONIC MAPS FROM PSEUDO-HERMITIAN MANIFOLDS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 234 / June 2019
- Published online by Cambridge University Press:
- 06 November 2017, pp. 170-210
- Print publication:
- June 2019
-
- Article
-
- You have access
- HTML
- Export citation
On the total mean curvature of a compact space-like submanifold in Lorentz–Minkowski spacetime
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 20 October 2017, pp. 199-210
- Print publication:
- February 2018
-
- Article
- Export citation
Closure of singular foliations: the proof ofMolino’s conjecture
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 12 / December 2017
- Published online by Cambridge University Press:
- 13 September 2017, pp. 2577-2590
- Print publication:
- December 2017
-
- Article
- Export citation
DISCRETE LINEAR WEINGARTEN SURFACES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 231 / September 2018
- Published online by Cambridge University Press:
- 04 September 2017, pp. 55-88
- Print publication:
- September 2018
-
- Article
-
- You have access
- HTML
- Export citation
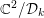
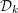
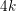
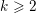

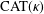
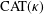
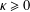
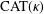
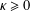
 =
=