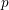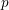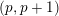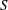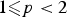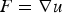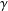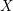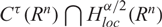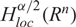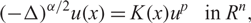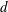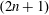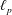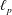Refine listing
Actions for selected content:
490 results in 53Cxx
GAUSSIAN CURVATURE AND UNICITY PROBLEM OF GAUSS MAPS OF VARIOUS CLASSES OF SURFACES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 240 / December 2020
- Published online by Cambridge University Press:
- 18 March 2019, pp. 275-297
- Print publication:
- December 2020
-
- Article
-
- You have access
- HTML
- Export citation
COMPLETE WEINGARTEN HYPERSURFACES SATISFYING AN OKUMURA TYPE INEQUALITY
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 109 / Issue 1 / August 2020
- Published online by Cambridge University Press:
- 11 March 2019, pp. 81-92
- Print publication:
- August 2020
-
- Article
-
- You have access
- Export citation
CHARACTERIZATIONS OF BERGER SPHERES FROM THE VIEWPOINT OF SUBMANIFOLD THEORY
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 62 / Issue 1 / January 2020
- Published online by Cambridge University Press:
- 01 March 2019, pp. 137-145
- Print publication:
- January 2020
-
- Article
-
- You have access
- Export citation
On local stabilities of
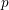 $p$-Kähler structures
$p$-Kähler structures
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 3 / March 2019
- Published online by Cambridge University Press:
- 07 March 2019, pp. 455-483
- Print publication:
- March 2019
-
- Article
- Export citation
Homogeneous Einstein Manifolds with Vanishing
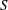 $S$ Curvature
$S$ Curvature
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 3 / September 2019
- Published online by Cambridge University Press:
- 22 February 2019, pp. 525-537
- Print publication:
- September 2019
-
- Article
-
- You have access
- Export citation
ON ODD-DIMENSIONAL COMPLEX ANALYTIC KLEINIAN GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 108 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 12 February 2019, pp. 1-32
- Print publication:
- February 2020
-
- Article
-
- You have access
- Export citation
Analytic and geometric properties of dislocation singularities
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 4 / August 2020
- Published online by Cambridge University Press:
- 01 February 2019, pp. 1609-1651
- Print publication:
- August 2020
-
- Article
- Export citation
A COMPACTNESS PRINCIPLE FOR MAXIMISING SMOOTH FUNCTIONS OVER TOROIDAL GEODESICS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 1 / August 2019
- Published online by Cambridge University Press:
- 01 February 2019, pp. 148-154
- Print publication:
- August 2019
-
- Article
-
- You have access
- Export citation
Nonabelian Hodge theory for klt spaces and descent theorems for vector bundles
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 2 / February 2019
- Published online by Cambridge University Press:
- 07 February 2019, pp. 289-323
- Print publication:
- February 2019
-
- Article
- Export citation
ON NONLOCAL NONLINEAR ELLIPTIC PROBLEMS WITH THE FRACTIONAL LAPLACIAN
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 62 / Issue 1 / January 2020
- Published online by Cambridge University Press:
- 29 January 2019, pp. 75-84
- Print publication:
- January 2020
-
- Article
-
- You have access
- Export citation
Existence and non-existence of minimal graphic and p-harmonic functions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 25 January 2019, pp. 341-366
- Print publication:
- February 2020
-
- Article
- Export citation
Non-collapsing in homogeneity greater than one via a two-point method for a special case
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 6 / December 2019
- Published online by Cambridge University Press:
- 24 January 2019, pp. 1627-1635
- Print publication:
- December 2019
-
- Article
- Export citation
Quantitative estimates for bending energies and applications to non-local variational problems
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 23 January 2019, pp. 131-169
- Print publication:
- February 2020
-
- Article
- Export citation
A note on rigidity theorem of λ-hypersurfaces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 6 / December 2019
- Published online by Cambridge University Press:
- 18 January 2019, pp. 1595-1601
- Print publication:
- December 2019
-
- Article
- Export citation
Codimension two spacelike submanifolds of the Lorentz-Minkowski spacetime into the light cone
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 6 / December 2019
- Published online by Cambridge University Press:
- 17 January 2019, pp. 1523-1553
- Print publication:
- December 2019
-
- Article
- Export citation
Generating Curves of Minimal Ruled Real Hypersurfaces in a Nonflat Complex Space Form
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 2 / June 2019
- Published online by Cambridge University Press:
- 09 January 2019, pp. 383-392
- Print publication:
- June 2019
-
- Article
-
- You have access
- Export citation
METRICS AND SPECIAL KÄHLER GEOMETRY ON THE MODULI SPACES OF HIGGS BUNDLES ANDHITCHIN SYSTEMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 2 / April 2019
- Published online by Cambridge University Press:
- 07 January 2019, pp. 340-341
- Print publication:
- April 2019
-
- Article
-
- You have access
- Export citation
A CR Analogue of Yau’s Conjecture on Pseudoharmonic Functions of Polynomial Growth
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 6 / December 2019
- Published online by Cambridge University Press:
- 07 January 2019, pp. 1367-1394
- Print publication:
- December 2019
-
- Article
-
- You have access
- Export citation
Finsler Warped Product Metrics of Douglas Type
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 1 / March 2019
- Published online by Cambridge University Press:
- 04 January 2019, pp. 119-130
- Print publication:
- March 2019
-
- Article
-
- You have access
- Export citation
On the Metric Compactification of Infinite-dimensional
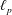 $\ell _{p}$ Spaces
$\ell _{p}$ Spaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 3 / September 2019
- Published online by Cambridge University Press:
- 28 December 2018, pp. 491-507
- Print publication:
- September 2019
-
- Article
-
- You have access
- Export citation