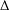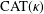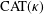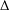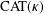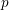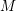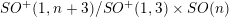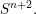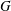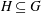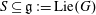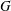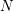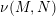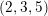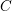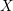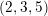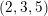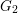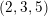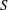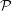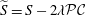Refine listing
Actions for selected content:
491 results in 53Cxx
Hardy type inequalities on closed manifolds via Ricci curvature
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 3 / June 2021
- Published online by Cambridge University Press:
- 21 July 2020, pp. 993-1020
- Print publication:
- June 2021
-
- Article
- Export citation
GRADIENT ESTIMATES VIA TWO-POINT FUNCTIONS FOR PARABOLIC EQUATIONS UNDER RICCI FLOW
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 2 / October 2020
- Published online by Cambridge University Press:
- 10 June 2020, pp. 319-330
- Print publication:
- October 2020
-
- Article
-
- You have access
- Export citation
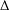 $\unicode[STIX]{x1D6E5}$-CONVERGENCES OF WEIGHTED AVERAGED PROJECTIONS IN
$\unicode[STIX]{x1D6E5}$-CONVERGENCES OF WEIGHTED AVERAGED PROJECTIONS IN 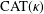 $\text{CAT}(\unicode[STIX]{x1D705})$ SPACES
$\text{CAT}(\unicode[STIX]{x1D705})$ SPACES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 110 / Issue 3 / June 2021
- Published online by Cambridge University Press:
- 14 May 2020, pp. 289-301
-
- Article
- Export citation
Finsler Warped Product Metrics with Relatively Isotropic Landsberg Curvature
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 12 May 2020, pp. 182-191
- Print publication:
- March 2021
-
- Article
-
- You have access
- Export citation
WEIERSTRASS–KENMOTSU REPRESENTATION OF WILLMORE SURFACES IN SPHERES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 244 / December 2021
- Published online by Cambridge University Press:
- 27 April 2020, pp. 35-59
-
- Article
- Export citation
DEFORMING A STARSHAPED CURVE INTO A CIRCLE BY AN AREA-PRESERVING FLOW
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 3 / December 2020
- Published online by Cambridge University Press:
- 23 April 2020, pp. 498-505
- Print publication:
- December 2020
-
- Article
-
- You have access
- Export citation
FOUR-MANIFOLDS WITH POSITIVE CURVATURE
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 63 / Issue 2 / May 2021
- Published online by Cambridge University Press:
- 06 April 2020, pp. 245-257
-
- Article
- Export citation
Reflection of Willmore Surfaces with Free Boundaries
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 3 / June 2021
- Published online by Cambridge University Press:
- 11 March 2020, pp. 787-804
- Print publication:
- June 2021
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ANCIENT SOLUTIONS OF CODIMENSION TWO SURFACES WITH CURVATURE PINCHING - RETRACTED
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 1 / August 2020
- Published online by Cambridge University Press:
- 06 March 2020, pp. 162-171
- Print publication:
- August 2020
-
- Article
-
- You have access
- Export citation
An Application of Spherical Geometry to Hyperkähler Slices
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 3 / June 2021
- Published online by Cambridge University Press:
- 24 February 2020, pp. 687-716
- Print publication:
- June 2021
-
- Article
- Export citation
Moduli Spaces of Metrics of Positive Scalar Curvature on Topological Spherical Space Forms
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 24 February 2020, pp. 901-908
- Print publication:
- December 2020
-
- Article
-
- You have access
- Open access
- Export citation
Deformation spaces and normal forms around transversals
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 4 / April 2020
- Published online by Cambridge University Press:
- 17 February 2020, pp. 697-732
- Print publication:
- April 2020
-
- Article
- Export citation
Topological mixing of Weyl chamber flows
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 5 / May 2021
- Published online by Cambridge University Press:
- 17 February 2020, pp. 1342-1368
- Print publication:
- May 2021
-
- Article
- Export citation
Short closed geodesics with self-intersections
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 169 / Issue 3 / November 2020
- Published online by Cambridge University Press:
- 24 January 2020, pp. 623-638
- Print publication:
- November 2020
-
- Article
- Export citation
DUALITY OF (2, 3, 5)-DISTRIBUTIONS AND LAGRANGIAN CONE STRUCTURES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 243 / September 2021
- Published online by Cambridge University Press:
- 23 January 2020, pp. 303-315
-
- Article
- Export citation
Metrizability of Holonomy Invariant Projective Deformation of Sprays
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 23 January 2020, pp. 701-714
- Print publication:
- September 2023
-
- Article
- Export citation
EXISTENCE AND COMPACTNESS THEORY FOR ALE SCALAR-FLAT KÄHLER SURFACES
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 10 January 2020, e1
-
- Article
-
- You have access
- Open access
- Export citation
Nearly Parallel G2-structures with Large Symmetry Group
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 16 December 2019, pp. 339-359
- Print publication:
- April 2021
-
- Article
- Export citation
Open problems and questions about geodesics
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 3 / March 2021
- Published online by Cambridge University Press:
- 06 December 2019, pp. 641-684
- Print publication:
- March 2021
-
- Article
- Export citation
Simplicial complexity of surface groups
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 6 / December 2020
- Published online by Cambridge University Press:
- 27 November 2019, pp. 3153-3162
- Print publication:
- December 2020
-
- Article
- Export citation