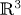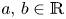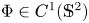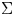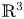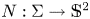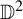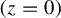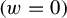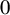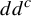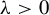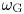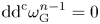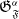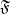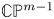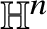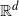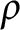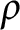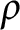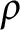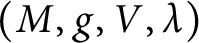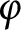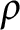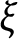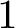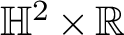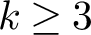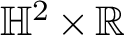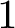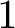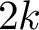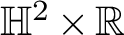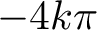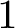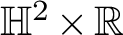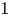Refine listing
Actions for selected content:
491 results in 53Cxx
Surfaces of prescribed linear Weingarten curvature in $\mathbb {R}^{3}$
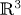
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 4 / August 2023
- Published online by Cambridge University Press:
- 22 July 2022, pp. 1347-1370
- Print publication:
- August 2023
-
- Article
- Export citation
Homogeneous and curvature homogeneous Lorentzian critical metrics
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 4 / August 2023
- Published online by Cambridge University Press:
- 08 July 2022, pp. 1272-1296
- Print publication:
- August 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Directed harmonic currents near non-hyperbolic linearizable singularities
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 7 / July 2023
- Published online by Cambridge University Press:
- 07 July 2022, pp. 2228-2257
- Print publication:
- July 2023
-
- Article
- Export citation
Numerically non-special varieties
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 6 / June 2022
- Published online by Cambridge University Press:
- 22 August 2022, pp. 1428-1447
- Print publication:
- June 2022
-
- Article
- Export citation
Singular Gauduchon metrics
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 6 / June 2022
- Published online by Cambridge University Press:
- 17 August 2022, pp. 1314-1328
- Print publication:
- June 2022
-
- Article
- Export citation
Characterization of totally geodesic foliations with integrable and parallelizable normal bundle
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 10 May 2022, pp. 128-137
-
- Article
- Export citation
Non-Hilbertian tangents to Hilbertian spaces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 05 April 2022, pp. 811-832
- Print publication:
- June 2023
-
- Article
- Export citation
A note on holomorphic sectional curvature of a hermitian manifold
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 04 March 2022, pp. 739-745
-
- Article
- Export citation
Computing harmonic maps between Riemannian manifolds
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 18 February 2022, pp. 531-580
- Print publication:
- April 2023
-
- Article
- Export citation
On cohomogeneity one Hermitian non-Kähler metrics
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 17 February 2022, pp. 545-587
- Print publication:
- April 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Continuity of critical exponent of quasiconvex-cocompact groups under Gromov–Hausdorff convergence
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 4 / April 2023
- Published online by Cambridge University Press:
- 10 February 2022, pp. 1189-1221
- Print publication:
- April 2023
-
- Article
- Export citation
Lipschitz graphs and currents in Heisenberg groups
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 02 February 2022, e6
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On complete submanifolds with parallel normalized mean curvature in product spaces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 27 January 2022, pp. 331-355
- Print publication:
- April 2022
-
- Article
- Export citation
Intersections of random sets
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 17 January 2022, pp. 131-151
- Print publication:
- March 2022
-
- Article
- Export citation
Some characterizations of
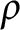 $\rho $-Einstein solitons on Sasakian manifolds
$\rho $-Einstein solitons on Sasakian manifolds
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 17 January 2022, pp. 1036-1049
- Print publication:
- December 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
GENUS
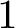 $1$ MINIMAL k-NOIDS AND SADDLE TOWERS IN
$1$ MINIMAL k-NOIDS AND SADDLE TOWERS IN 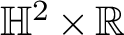 $\mathbb {H}^2\times \mathbb {R}$
$\mathbb {H}^2\times \mathbb {R}$
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 5 / September 2023
- Published online by Cambridge University Press:
- 06 January 2022, pp. 2155-2175
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Index estimates for closed minimal submanifolds of the sphere
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 17 December 2021, pp. 802-816
- Print publication:
- June 2022
-
- Article
- Export citation
On pull-backs of the universal connection
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 10 December 2021, pp. 845-859
- Print publication:
- December 2022
-
- Article
- Export citation
Carnot metrics, dynamics and local rigidity
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 2 / February 2022
- Published online by Cambridge University Press:
- 09 December 2021, pp. 614-664
- Print publication:
- February 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Eisenstein metrics
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 03 December 2021, pp. 778-803
- Print publication:
- June 2023
-
- Article
- Export citation