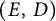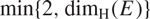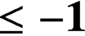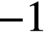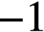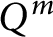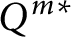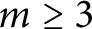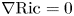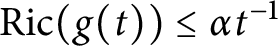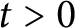Refine listing
Actions for selected content:
490 results in 53Cxx
A NOTE ON THE CLASSIFICATION OF NONCOMPACT QUASI-EINSTEIN MANIFOLDS WITH VANISHING CONDITION ON THE WEYL TENSOR
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 2 / May 2022
- Published online by Cambridge University Press:
- 07 May 2021, pp. 336-346
- Print publication:
- May 2022
-
- Article
- Export citation
A min-max characterization of Zoll Riemannian metrics
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 172 / Issue 3 / May 2022
- Published online by Cambridge University Press:
- 29 April 2021, pp. 591-615
- Print publication:
- May 2022
-
- Article
- Export citation
On certain Tannakian categories of integrable connections over Kähler manifolds
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 4 / August 2022
- Published online by Cambridge University Press:
- 21 April 2021, pp. 1034-1061
- Print publication:
- August 2022
-
- Article
- Export citation
Projections of Poisson cut-outs in the Heisenberg group and the visual 3-sphere
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 172 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 08 March 2021, pp. 197-230
- Print publication:
- January 2022
-
- Article
- Export citation
Uniqueness of optimal symplectic connections
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 04 March 2021, e18
-
- Article
-
- You have access
- Open access
- Export citation
REALIZING METRICS OF CURVATURE
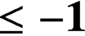 $\mathbf {\leq -1}$ ON CLOSED SURFACES IN FUCHSIAN ANTI-DE SITTER MANIFOLDS
$\mathbf {\leq -1}$ ON CLOSED SURFACES IN FUCHSIAN ANTI-DE SITTER MANIFOLDS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 112 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 19 February 2021, pp. 312-334
- Print publication:
- June 2022
-
- Article
- Export citation
Non-existence of conformally flat real hypersurfaces in both the complex quadric and the complex hyperbolic quadric
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 15 February 2021, pp. 68-83
- Print publication:
- March 2022
-
- Article
- Export citation
On the first eigenvalue of the Laplace operator for compact spacelike submanifolds in Lorentz–Minkowski spacetime 𝕃m
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 11 February 2021, pp. 311-330
- Print publication:
- April 2022
-
- Article
- Export citation
Sharp Caffarelli–Kohn–Nirenberg inequalities on Riemannian manifolds: the influence of curvature
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 22 January 2021, pp. 102-127
- Print publication:
- February 2022
-
- Article
- Export citation
LOSIK CLASSES FOR CODIMENSION-ONE FOLIATIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 4 / July 2022
- Published online by Cambridge University Press:
- 08 January 2021, pp. 1391-1419
- Print publication:
- July 2022
-
- Article
- Export citation
Prescribed k-symmetric curvature hypersurfaces in de Sitter space
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 26 November 2020, pp. 886-901
- Print publication:
- December 2021
-
- Article
- Export citation
A new classification on parallel Ricci tensor for real hypersurfaces in the complex quadric
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 6 / December 2021
- Published online by Cambridge University Press:
- 18 November 2020, pp. 1846-1868
- Print publication:
- December 2021
-
- Article
- Export citation
RC-positive metrics on rationally connected manifolds
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 16 November 2020, e53
-
- Article
-
- You have access
- Open access
- Export citation
Some local maximum principles along Ricci flows
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 04 November 2020, pp. 329-348
- Print publication:
- April 2022
-
- Article
- Export citation
Lagrangian foliations and Anosov symplectomorphisms on Kähler manifolds
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 11 / November 2021
- Published online by Cambridge University Press:
- 30 October 2020, pp. 3325-3335
- Print publication:
- November 2021
-
- Article
-
- You have access
- Open access
- Export citation
REAL HYPERSURFACES IN COMPLEX SPACE FORMS ATTAINING EQUALITY IN AN INEQUALITY INVOLVING A CONTACT δ-INVARIANT
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 63 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 24 September 2020, pp. 724-731
- Print publication:
- September 2021
-
- Article
- Export citation
Some results on Ricci-Bourguignon solitons and almost solitons
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 20 August 2020, pp. 591-604
- Print publication:
- September 2021
-
- Article
- Export citation
Minimizing movements for forced anisotropic mean curvature flow of partitions with mobilities
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 4 / August 2021
- Published online by Cambridge University Press:
- 17 August 2020, pp. 1135-1170
- Print publication:
- August 2021
-
- Article
-
- You have access
- Open access
- Export citation
PROJECTIVE LOOPS GENERATE RATIONAL LOOP GROUPS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 2 / March 2022
- Published online by Cambridge University Press:
- 17 August 2020, pp. 459-485
- Print publication:
- March 2022
-
- Article
- Export citation
Hardy type inequalities on closed manifolds via Ricci curvature
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 3 / June 2021
- Published online by Cambridge University Press:
- 21 July 2020, pp. 993-1020
- Print publication:
- June 2021
-
- Article
- Export citation