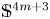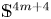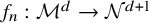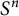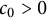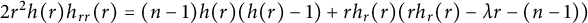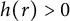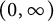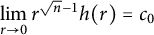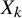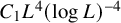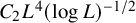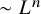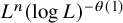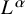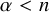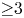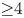Refine listing
Actions for selected content:
490 results in 53Cxx
Simplicial volume of manifolds with amenable fundamental group at infinity
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 66 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 22 April 2024, pp. 563-570
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Isochronous centers and flat Finsler metrics (I)
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 4 / August 2025
- Published online by Cambridge University Press:
- 15 April 2024, pp. 1294-1314
- Print publication:
- August 2025
-
- Article
- Export citation
On almost quotient Yamabe solitons
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 66 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 11 April 2024, pp. 479-493
- Print publication:
- September 2024
-
- Article
- Export citation
Buffon’s problem determines Gaussian curvature in three geometries
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 08 April 2024, pp. 1127-1138
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Positive Einstein metrics with
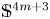 $\mathbb {S}^{4m+3}$ as the principal orbit
$\mathbb {S}^{4m+3}$ as the principal orbit
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 5 / May 2024
- Published online by Cambridge University Press:
- 08 April 2024, pp. 1004-1040
- Print publication:
- May 2024
-
- Article
- Export citation
Stability of isometric immersions of hypersurfaces
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 02 April 2024, e43
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Calibrated geometry in hyperkähler cones, 3-Sasakian manifolds, and twistor spaces
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 4 / August 2025
- Published online by Cambridge University Press:
- 01 April 2024, pp. 1163-1221
- Print publication:
- August 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Existence of singular rotationally symmetric gradient Ricci solitons in higher dimensions
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 21 March 2024, pp. 842-859
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A boundary maximum principle for stationary pairs of varifolds with fixed contact angle
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 2 / May 2024
- Published online by Cambridge University Press:
- 08 March 2024, pp. 316-335
-
- Article
- Export citation
Structure of generalized Yamabe solitons and its applications
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 2 / May 2024
- Published online by Cambridge University Press:
- 07 March 2024, pp. 336-348
-
- Article
- Export citation
Index estimates of compact hypersurfaces in smooth metric measure spaces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 5 / October 2025
- Published online by Cambridge University Press:
- 07 March 2024, pp. 1895-1913
- Print publication:
- October 2025
-
- Article
- Export citation
A class of Hessian quotient equations in de Sitter space
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 06 March 2024, pp. 805-821
- Print publication:
- September 2024
-
- Article
- Export citation
Degrees of maps and multiscale geometry
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 12 / 2024
- Published online by Cambridge University Press:
- 18 January 2024, e2
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Joint partial equidistribution of Farey rays in negatively curved manifolds and trees
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 9 / September 2024
- Published online by Cambridge University Press:
- 08 January 2024, pp. 2700-2736
- Print publication:
- September 2024
-
- Article
- Export citation
Positivity of Schur forms for strongly decomposably positive vector bundles
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 08 January 2024, e9
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Isoparametric hypersurfaces in symmetric spaces of non-compact type and higher rank
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 2 / February 2024
- Published online by Cambridge University Press:
- 05 January 2024, pp. 451-462
- Print publication:
- February 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On Calderon's problem for the connection Laplacian
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 05 January 2024, pp. 1087-1112
- Print publication:
- June 2025
-
- Article
- Export citation
A rigidity result for the product of spheres
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 13 December 2023, pp. 574-581
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the Pontrjagin classes of spray manifolds
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 11 December 2023, pp. 544-553
- Print publication:
- September 2024
-
- Article
- Export citation
A note on almost Yamabe solitons
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 66 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 29 November 2023, pp. 183-187
- Print publication:
- January 2024
-
- Article
- Export citation