Refine listing
Actions for selected content:
490 results in 53Cxx
Real hypersurfaces in the complex quadric with Killing normal Jacobi operator
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 2 / April 2019
- Published online by Cambridge University Press:
- 27 December 2018, pp. 279-296
- Print publication:
- April 2019
-
- Article
- Export citation
Lagrangian submanifolds of the nearly Kähler 𝕊3 × 𝕊3 from minimal surfaces in 𝕊3
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 3 / June 2019
- Published online by Cambridge University Press:
- 27 December 2018, pp. 655-689
- Print publication:
- June 2019
-
- Article
- Export citation
LARGE-SCALE SUBLINEARLY LIPSCHITZ GEOMETRY OF HYPERBOLIC SPACES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 6 / November 2020
- Published online by Cambridge University Press:
- 19 December 2018, pp. 1831-1876
- Print publication:
- November 2020
-
- Article
- Export citation
Higher rank rigidity for Berwald spaces
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 7 / July 2020
- Published online by Cambridge University Press:
- 18 December 2018, pp. 1991-2016
- Print publication:
- July 2020
-
- Article
- Export citation
Ricci Solitons on Almost Co-Kähler Manifolds
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 4 / December 2019
- Published online by Cambridge University Press:
- 07 December 2018, pp. 912-922
- Print publication:
- December 2019
-
- Article
-
- You have access
- Export citation
Gradient Estimates for Spacelike Mean Curvature Flow with Boundary Conditions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 2 / May 2019
- Published online by Cambridge University Press:
- 29 November 2018, pp. 459-469
-
- Article
- Export citation
On geodesic flows with symmetries and closed magnetic geodesics on orbifolds
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 6 / June 2020
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1480-1509
- Print publication:
- June 2020
-
- Article
- Export citation
A partial converse to the Andreotti–Grauert theorem
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 1 / January 2019
- Published online by Cambridge University Press:
- 19 November 2018, pp. 89-99
- Print publication:
- January 2019
-
- Article
- Export citation
Combinatorics of one-dimensional simple Toeplitz subshifts
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 6 / June 2020
- Published online by Cambridge University Press:
- 13 November 2018, pp. 1673-1714
- Print publication:
- June 2020
-
- Article
- Export citation
Holomorphic Vanishing Theorems on Finsler Holomorphic Vector Bundles and Complex Finsler Manifolds
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 3 / September 2019
- Published online by Cambridge University Press:
- 09 November 2018, pp. 623-641
- Print publication:
- September 2019
-
- Article
-
- You have access
- Export citation
Homogeneous Einstein Finsler Metrics on
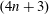 $(4n+3)$-dimensional Spheres
$(4n+3)$-dimensional Spheres
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 3 / September 2019
- Published online by Cambridge University Press:
- 09 November 2018, pp. 509-523
- Print publication:
- September 2019
-
- Article
-
- You have access
- Export citation
CONTACT METRIC THREE-MANIFOLDS WITH CONSTANT SCALAR TORSION
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 107 / Issue 2 / October 2019
- Published online by Cambridge University Press:
- 29 October 2018, pp. 234-255
- Print publication:
- October 2019
-
- Article
-
- You have access
- Export citation
Comparison Geometry of Manifolds with Boundary under a Lower Weighted Ricci Curvature Bound
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 24 October 2018, pp. 243-280
- Print publication:
- February 2020
-
- Article
-
- You have access
- Export citation
Hyperbolic rank rigidity for manifolds of
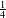 $\frac{1}{4}$-pinched negative curvature
$\frac{1}{4}$-pinched negative curvature
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 5 / May 2020
- Published online by Cambridge University Press:
- 08 October 2018, pp. 1194-1216
- Print publication:
- May 2020
-
- Article
- Export citation
A Class of Parabolic Equations Driven by the Mean Curvature Flow
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 30 August 2018, pp. 135-163
-
- Article
- Export citation
Geodesic Flows Modelled by Expansive Flows
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 28 August 2018, pp. 61-95
-
- Article
- Export citation
ENTIRE SOLUTIONS OF A CURVATURE FLOW IN AN UNDULATING CYLINDER
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 15 August 2018, pp. 137-147
- Print publication:
- February 2019
-
- Article
-
- You have access
- Export citation
DYNAMIC ISOPERIMETRY ON GRAPHS AND WEIGHTED RIEMANNIAN MANIFOLDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 3 / December 2018
- Published online by Cambridge University Press:
- 15 August 2018, pp. 514-515
- Print publication:
- December 2018
-
- Article
-
- You have access
- Export citation
Geometry and topology of the space of Kähler metrics on singular varieties
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 8 / August 2018
- Published online by Cambridge University Press:
- 19 July 2018, pp. 1593-1632
- Print publication:
- August 2018
-
- Article
- Export citation
Space-like hypersurfaces with functionally bounded mean curvature in Lorentzian warped products and generalized Calabi–Bernstein-type problems
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 4 / August 2019
- Published online by Cambridge University Press:
- 22 June 2018, pp. 849-868
- Print publication:
- August 2019
-
- Article
- Export citation
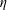
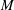
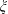
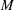
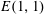
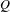
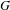
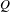
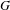
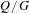
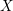
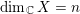
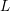
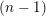
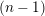
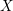
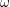
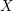
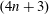
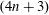
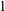
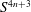
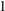
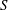
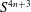
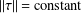
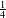
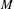
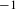
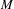
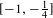
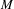
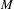

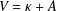
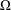
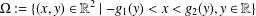
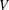
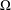

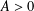
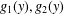
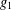
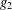
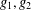
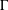
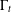
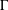
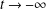
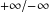
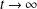
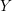
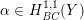
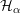
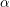
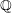
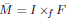 , where
, where 