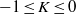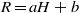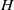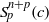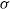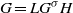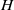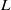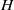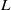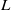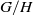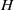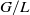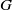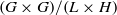Refine listing
Actions for selected content:
483 results in 53Cxx
MINIMAL VOLUME OF COMPLETE UNIFORM VISIBILITY MANIFOLDS WITH FINITE VOLUME
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 94 / Issue 3 / June 2013
- Published online by Cambridge University Press:
- 07 June 2013, pp. 375-384
- Print publication:
- June 2013
-
- Article
-
- You have access
- Export citation
On the classification of the real vector subspaces of a quaternionic vector space
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 56 / Issue 2 / June 2013
- Published online by Cambridge University Press:
- 03 April 2013, pp. 615-622
-
- Article
-
- You have access
- Export citation
On generalized Gauduchon metrics
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 56 / Issue 3 / October 2013
- Published online by Cambridge University Press:
- 21 March 2013, pp. 733-753
-
- Article
-
- You have access
- Export citation
A vanishing theorem in twisted de Rham cohomology
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 56 / Issue 2 / June 2013
- Published online by Cambridge University Press:
- 20 March 2013, pp. 501-508
-
- Article
-
- You have access
- Export citation
COMPLETE SPACELIKE SUBMANIFOLDS IN DE SITTER SPACES WITH
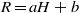 $R= aH+ b$
$R= aH+ b$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 87 / Issue 3 / June 2013
- Published online by Cambridge University Press:
- 13 February 2013, pp. 386-399
- Print publication:
- June 2013
-
- Article
-
- You have access
- Export citation
The standard conjectures for holomorphic symplectic varieties deformation equivalent to Hilbert schemes of K3 surfaces
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 3 / March 2013
- Published online by Cambridge University Press:
- 07 February 2013, pp. 481-494
- Print publication:
- March 2013
-
- Article
- Export citation
SLANT CURVES AND PARTICLES IN THREE-DIMENSIONAL WARPED PRODUCTS AND THEIR LANCRET INVARIANTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 88 / Issue 1 / August 2013
- Published online by Cambridge University Press:
- 19 October 2012, pp. 128-142
- Print publication:
- August 2013
-
- Article
-
- You have access
- Export citation
Index theorems on manifolds with straight ends
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 6 / November 2012
- Published online by Cambridge University Press:
- 15 October 2012, pp. 1897-1968
- Print publication:
- November 2012
-
- Article
-
- You have access
- Export citation
On the limit behavior of metrics in the continuity method for the Kähler–Einstein problem on a toric Fano manifold
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 6 / November 2012
- Published online by Cambridge University Press:
- 12 October 2012, pp. 1985-2003
- Print publication:
- November 2012
-
- Article
-
- You have access
- Export citation
VISIBLE ACTIONS ON FLAG VARIETIES OF TYPE B AND A GENERALISATION OF THE CARTAN DECOMPOSITION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 88 / Issue 1 / August 2013
- Published online by Cambridge University Press:
- 20 August 2012, pp. 81-97
- Print publication:
- August 2013
-
- Article
-
- You have access
- Export citation
Harmonic maps between rotationally symmetric manifolds
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 55 / Issue 3 / October 2012
- Published online by Cambridge University Press:
- 26 July 2012, pp. 685-695
-
- Article
-
- You have access
- Export citation
TRANSVERSAL INFINITESIMAL AUTOMORPHISMS ON KÄHLER FOLIATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 86 / Issue 3 / December 2012
- Published online by Cambridge University Press:
- 02 February 2012, pp. 405-415
- Print publication:
- December 2012
-
- Article
-
- You have access
- Export citation
Invariant valuations on quaternionic vector spaces
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 11 / Issue 3 / July 2012
- Published online by Cambridge University Press:
- 24 January 2012, pp. 467-499
- Print publication:
- July 2012
-
- Article
- Export citation
BIHARMONIC SUBMANIFOLDS IN NONFLAT LORENTZ 3-SPACE FORMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 85 / Issue 3 / June 2012
- Published online by Cambridge University Press:
- 30 November 2011, pp. 422-432
- Print publication:
- June 2012
-
- Article
-
- You have access
- Export citation
Kähler groups, real hyperbolic spaces and the Cremona group. With an appendix by Serge Cantat
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 1 / January 2012
- Published online by Cambridge University Press:
- 30 November 2011, pp. 153-184
- Print publication:
- January 2012
-
- Article
-
- You have access
- Export citation
H-CONTACT UNIT TANGENT SPHERE BUNDLES OF FOUR-DIMENSIONAL RIEMANNIAN MANIFOLDS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 91 / Issue 2 / October 2011
- Published online by Cambridge University Press:
- 21 September 2011, pp. 243-256
- Print publication:
- October 2011
-
- Article
-
- You have access
- Export citation
Existence and non-uniqueness of constant scalar curvature toric Sasaki metrics
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 5 / September 2011
- Published online by Cambridge University Press:
- 27 July 2011, pp. 1613-1634
- Print publication:
- September 2011
-
- Article
-
- You have access
- Export citation
ON MINIMAL SURFACES SATISFYING THE OMORI–YAU PRINCIPLE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 84 / Issue 1 / August 2011
- Published online by Cambridge University Press:
- 16 June 2011, pp. 33-39
- Print publication:
- August 2011
-
- Article
-
- You have access
- Export citation
Location of geodesics and isoperimetric inequalities in Denjoy domains
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 55 / Issue 1 / February 2012
- Published online by Cambridge University Press:
- 15 June 2011, pp. 245-269
-
- Article
-
- You have access
- Export citation
INVARIANT EINSTEIN METRICS ON GENERALIZED FLAG MANIFOLDS WITH TWO ISOTROPY SUMMANDS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 90 / Issue 2 / April 2011
- Published online by Cambridge University Press:
- 19 July 2011, pp. 237-251
- Print publication:
- April 2011
-
- Article
-
- You have access
- Export citation