Refine listing
Actions for selected content:
56 results in 12Exx
ON PERMUTATION BINOMIALS OVER FINITE FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 89 / Issue 1 / February 2014
- Published online by Cambridge University Press:
- 28 March 2013, pp. 112-124
- Print publication:
- February 2014
-
- Article
-
- You have access
- Export citation
ON THE EQUATION f(g(x))=f(x)hm(x) FOR COMPOSITE POLYNOMIALS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 92 / Issue 2 / April 2012
- Published online by Cambridge University Press:
- 19 September 2012, pp. 155-161
- Print publication:
- April 2012
-
- Article
-
- You have access
- Export citation
Hilbertianity of fields of power series
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 11 / Issue 2 / April 2012
- Published online by Cambridge University Press:
- 13 December 2011, pp. 351-361
- Print publication:
- April 2012
-
- Article
- Export citation
On the birational p-adic section conjecture
- Part of
-
- Journal:
- Compositio Mathematica / Volume 146 / Issue 3 / May 2010
- Published online by Cambridge University Press:
- 18 March 2010, pp. 621-637
- Print publication:
- May 2010
-
- Article
-
- You have access
- Export citation
Diamonds in Torsion of Abelian Varieties
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 9 / Issue 3 / July 2010
- Published online by Cambridge University Press:
- 10 February 2010, pp. 477-480
- Print publication:
- July 2010
-
- Article
- Export citation
Produit eulérien motivique et courbes rationnelles sur les variétés toriques
- Part of
-
- Journal:
- Compositio Mathematica / Volume 145 / Issue 6 / November 2009
- Published online by Cambridge University Press:
- 03 December 2009, pp. 1360-1400
- Print publication:
- November 2009
-
- Article
-
- You have access
- Export citation
Harmonic and equianharmonic equations in the Grothendieck–Teichmüller group. III
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 9 / Issue 2 / April 2010
- Published online by Cambridge University Press:
- 11 August 2009, pp. 431-448
- Print publication:
- April 2010
-
- Article
- Export citation
Problèmes de ruine en théorie du risque à temps discret avec horizon fini
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 40 / Issue 3 / September 2003
- Published online by Cambridge University Press:
- 14 July 2016, pp. 527-542
- Print publication:
- September 2003
-
- Article
- Export citation
Probabilité de ruine éventuelle dans un modèle de risque à temps discret
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 40 / Issue 3 / September 2003
- Published online by Cambridge University Press:
- 14 July 2016, pp. 543-556
- Print publication:
- September 2003
-
- Article
- Export citation
On extensions generated by roots of lifting polynomials
- Part of
-
- Journal:
- Mathematika / Volume 49 / Issue 1-2 / June 2002
- Published online by Cambridge University Press:
- 26 February 2010, pp. 107-118
- Print publication:
- June 2002
-
- Article
- Export citation
Difference polynomials and their generalizations
- Part of
-
- Journal:
- Mathematika / Volume 48 / Issue 1-2 / December 2001
- Published online by Cambridge University Press:
- 26 February 2010, pp. 293-299
- Print publication:
- December 2001
-
- Article
- Export citation
Factorization over local fields and the irreducibility of generalized difference polynomials
- Part of
-
- Journal:
- Mathematika / Volume 47 / Issue 1-2 / December 2000
- Published online by Cambridge University Press:
- 26 February 2010, pp. 173-196
- Print publication:
- December 2000
-
- Article
- Export citation
The orders of nonsingular derivations
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 67 / Issue 2 / October 1999
- Published online by Cambridge University Press:
- 09 April 2009, pp. 254-260
- Print publication:
- October 1999
-
- Article
-
- You have access
- Export citation
Representation formulas for entire functions of exponential type and generalized bernoulli polynomials
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 64 / Issue 3 / June 1998
- Published online by Cambridge University Press:
- 09 April 2009, pp. 307-316
- Print publication:
- June 1998
-
- Article
-
- You have access
- Export citation
On a generalization of Eisenstein's irreducibility criterion
- Part of
-
- Journal:
- Mathematika / Volume 44 / Issue 1 / June 1997
- Published online by Cambridge University Press:
- 26 February 2010, pp. 37-41
- Print publication:
- June 1997
-
- Article
- Export citation
On Schur's conjecture
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 58 / Issue 3 / June 1995
- Published online by Cambridge University Press:
- 09 April 2009, pp. 312-357
- Print publication:
- June 1995
-
- Article
-
- You have access
- Export citation
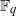
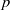
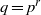
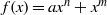
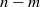
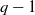
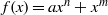
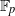
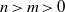
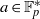
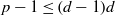
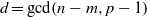
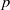
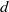
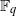
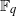
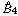 . A consequence is to represent a matrix specialization of the ‘equianharmonic’ parameter in terms of special values of the adelic beta function introduced and studied by Anderson and Ihara.
. A consequence is to represent a matrix specialization of the ‘equianharmonic’ parameter in terms of special values of the adelic beta function introduced and studied by Anderson and Ihara.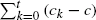 is bounded as the time
is bounded as the time 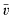 its unique prolongation to a fixed algebraic closure
its unique prolongation to a fixed algebraic closure 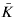 of
of 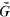 . For any subfield
. For any subfield 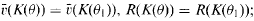 in case (
in case (