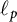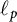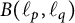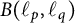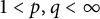Refine listing
Actions for selected content:
291 results in 46Bxx
On the class of weak U-Dunford–Pettis operators
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 12 November 2025, pp. 1-13
-
- Article
- Export citation
Regular Dilations on Kreĭn Spaces
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 03 November 2025, pp. 1-24
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A remark on characterizing inner product spaces via strong three-point homogeneity
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 30 October 2025, pp. 1-11
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Banach lattices of positively homogeneous functions induced by a Banach space
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society , First View
- Published online by Cambridge University Press:
- 27 October 2025, pp. 1-37
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The super Alternative Daugavet property for Banach spaces
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society , First View
- Published online by Cambridge University Press:
- 15 October 2025, pp. 1-29
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Study of weaving frames in Krein spaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 19 September 2025, pp. 1-16
-
- Article
- Export citation
Some characterizations of unbounded Dunford–Pettis operators
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 15 September 2025, pp. 1-8
-
- Article
- Export citation
ZOO OF IDEAL SCHAUDER BASES
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 05 September 2025, pp. 1-31
-
- Article
- Export citation
PROPERTY (T) AND STRONG 1-BOUNDEDNESS FOR VON NEUMANN ALGEBRAS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu , First View
- Published online by Cambridge University Press:
- 01 September 2025, pp. 1-34
-
- Article
- Export citation
Moduli of local uniform rotundity for convex bodies in normed spaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 4 / December 2025
- Published online by Cambridge University Press:
- 10 April 2025, pp. 1251-1261
- Print publication:
- December 2025
-
- Article
- Export citation
Zero-one law of orbital limit points for weighted shifts
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 3 / August 2025
- Published online by Cambridge University Press:
- 07 April 2025, pp. 945-978
-
- Article
- Export citation
A logarithmic uncertainty principle for functions with radial symmetry
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 3 / August 2025
- Published online by Cambridge University Press:
- 31 March 2025, pp. 811-824
-
- Article
- Export citation
Compact composition operators on model spaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 4 / December 2025
- Published online by Cambridge University Press:
- 18 March 2025, pp. 1109-1115
- Print publication:
- December 2025
-
- Article
- Export citation
Hyperbolic Metric Spaces and Stochastic Embeddings
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 07 February 2025, e29
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On several dynamical properties of shifts acting on directed trees
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 09 January 2025, pp. 1-30
-
- Article
- Export citation
A characterization of inner product spaces via norming vectors
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 03 January 2025, pp. 598-602
- Print publication:
- June 2025
-
- Article
- Export citation
Differentiability of the operator norm on
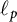 $\ell _p$ spaces
$\ell _p$ spaces
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 16 December 2024, pp. 1-20
-
- Article
- Export citation
On the complete separation of unique
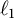 $\ell _{1}$ spreading models and the Lebesgue property of Banach spaces
$\ell _{1}$ spreading models and the Lebesgue property of Banach spaces
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 13 December 2024, pp. 1-23
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The Daugavet and Delta-constants of points in Banach spaces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 12 December 2024, pp. 1-35
-
- Article
- Export citation
Tilings of the hyperbolic space and Lipschitz functions
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 6 / December 2025
- Published online by Cambridge University Press:
- 18 November 2024, pp. 1985-2005
- Print publication:
- December 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation