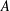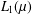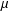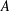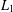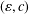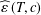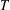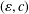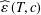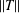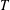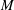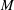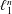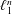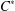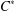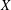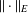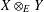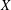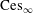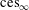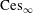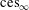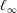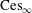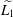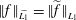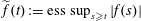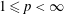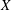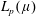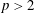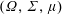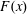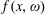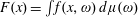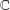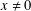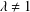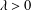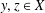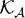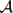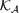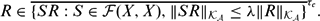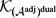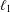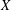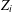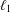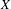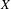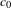Refine listing
Actions for selected content:
291 results in 46Bxx
A QUANTITATIVE EXTENSION OF SZLENK’S THEOREM
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 2 / October 2019
- Published online by Cambridge University Press:
- 20 February 2019, pp. 338-343
- Print publication:
- October 2019
-
- Article
-
- You have access
- Export citation
APPROXIMATELY ANGLE PRESERVING MAPPINGS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 3 / June 2019
- Published online by Cambridge University Press:
- 14 February 2019, pp. 485-496
- Print publication:
- June 2019
-
- Article
-
- You have access
- Export citation
Lipschitz-free Spaces on Finite Metric Spaces
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 13 February 2019, pp. 774-804
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation
APPROXIMATIONS OF SUBHOMOGENEOUS ALGEBRAS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 2 / October 2019
- Published online by Cambridge University Press:
- 07 February 2019, pp. 328-337
- Print publication:
- October 2019
-
- Article
-
- You have access
- Export citation
On a second numerical index for Banach spaces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 28 January 2019, pp. 1003-1051
- Print publication:
- April 2020
-
- Article
- Export citation
GEOMETRIC AND FIXED POINT PROPERTIES IN PRODUCTS OF NORMED SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 2 / April 2019
- Published online by Cambridge University Press:
- 10 January 2019, pp. 262-273
- Print publication:
- April 2019
-
- Article
-
- You have access
- Export citation
Quotients of Essentially Euclidean Spaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 1 / March 2019
- Published online by Cambridge University Press:
- 09 January 2019, pp. 71-74
- Print publication:
- March 2019
-
- Article
-
- You have access
- Export citation
Isomorphic Structure of Cesàro and Tandori Spaces
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 3 / June 2019
- Published online by Cambridge University Press:
- 09 January 2019, pp. 501-532
- Print publication:
- June 2019
-
- Article
-
- You have access
- Export citation
On the Metric Compactification of Infinite-dimensional
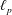 $\ell _{p}$ Spaces
$\ell _{p}$ Spaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 3 / September 2019
- Published online by Cambridge University Press:
- 28 December 2018, pp. 491-507
- Print publication:
- September 2019
-
- Article
-
- You have access
- Export citation
CONCERNING SUMMABLE SZLENK INDEX
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 62 / Issue 1 / January 2020
- Published online by Cambridge University Press:
- 21 December 2018, pp. 59-73
- Print publication:
- January 2020
-
- Article
-
- You have access
- Export citation
On the Pointwise Bishop–Phelps–Bollobás Property for Operators
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 6 / December 2019
- Published online by Cambridge University Press:
- 17 October 2018, pp. 1421-1443
- Print publication:
- December 2019
-
- Article
-
- You have access
- Export citation
Krivine’s Function Calculus and Bochner Integration
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 3 / September 2019
- Published online by Cambridge University Press:
- 15 October 2018, pp. 663-669
- Print publication:
- September 2019
-
- Article
-
- You have access
- Export citation
LEFT SYMMETRIC POINTS FOR BIRKHOFF ORTHOGONALITY IN THE PREDUALSOF VON NEUMANN ALGEBRAS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 3 / December 2018
- Published online by Cambridge University Press:
- 28 August 2018, pp. 494-501
- Print publication:
- December 2018
-
- Article
-
- You have access
- Export citation
A CHARACTERISATION OF EUCLIDEAN NORMED PLANES VIA BISECTORS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 20 August 2018, pp. 121-129
- Print publication:
- February 2019
-
- Article
-
- You have access
- Export citation
SOME RESULTS OF THE
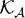 $\mathcal K_{\mathcal A}$-APPROXIMATION PROPERTY FOR BANACH SPACES
$\mathcal K_{\mathcal A}$-APPROXIMATION PROPERTY FOR BANACH SPACES
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 61 / Issue 3 / September 2019
- Published online by Cambridge University Press:
- 09 August 2018, pp. 545-555
- Print publication:
- September 2019
-
- Article
-
- You have access
- Export citation
FOURIER-TYPE TRANSFORMS ON REARRANGEMENT-INVARIANT QUASI-BANACH FUNCTION SPACES
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 61 / Issue 1 / January 2019
- Published online by Cambridge University Press:
- 20 June 2018, pp. 231-248
- Print publication:
- January 2019
-
- Article
-
- You have access
- Export citation
A WEAK HILBERT SPACE THAT IS A TWISTED HILBERT SPACE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 3 / May 2020
- Published online by Cambridge University Press:
- 15 May 2018, pp. 855-867
- Print publication:
- May 2020
-
- Article
- Export citation
NONEXPANSIVE BIJECTIONS TO THE UNIT BALL OF THE
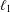 $\ell _{1}$ -SUM OF STRICTLY CONVEX BANACH SPACES
$\ell _{1}$ -SUM OF STRICTLY CONVEX BANACH SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 2 / April 2018
- Published online by Cambridge University Press:
- 20 February 2018, pp. 285-292
- Print publication:
- April 2018
-
- Article
-
- You have access
- Export citation
EQUIVALENT NORMS WITH AN EXTREMELY NONLINEABLE SET OF NORM ATTAINING FUNCTIONALS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 1 / January 2020
- Published online by Cambridge University Press:
- 13 February 2018, pp. 259-279
- Print publication:
- January 2020
-
- Article
- Export citation
DISTORTION IN THE FINITE DETERMINATION RESULT FOR EMBEDDINGS OF LOCALLY FINITE METRIC SPACES INTO BANACH SPACES
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 61 / Issue 1 / January 2019
- Published online by Cambridge University Press:
- 06 February 2018, pp. 33-47
- Print publication:
- January 2019
-
- Article
-
- You have access
- Export citation