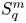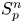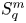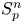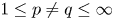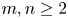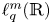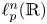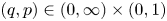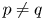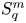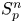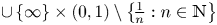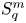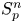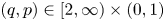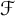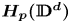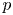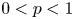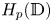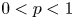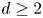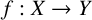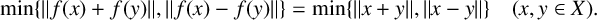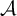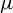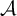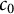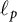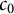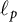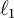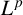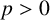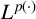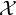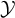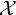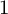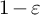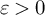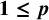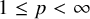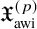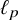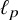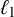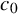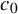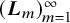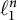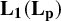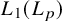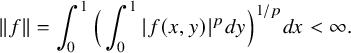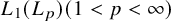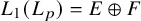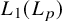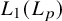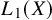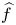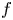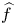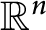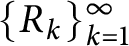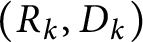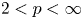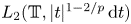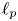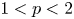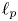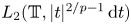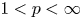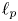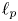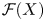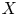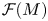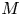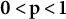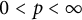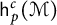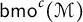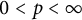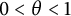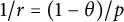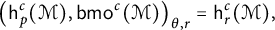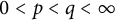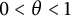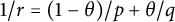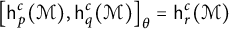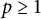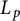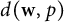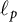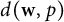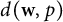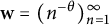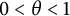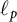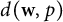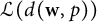Refine listing
Actions for selected content:
292 results in 46Bxx
On isometric embeddability of $S_q^m$
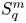 into $S_p^n$
into $S_p^n$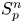 as non-commutative quasi-Banach spaces
as non-commutative quasi-Banach spaces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 4 / August 2024
- Published online by Cambridge University Press:
- 22 June 2023, pp. 1180-1203
- Print publication:
- August 2024
-
- Article
- Export citation
Schreier families and
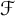 $\mathcal {F}$-(almost) greedy bases
$\mathcal {F}$-(almost) greedy bases
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 4 / August 2024
- Published online by Cambridge University Press:
- 14 June 2023, pp. 1379-1399
- Print publication:
- August 2024
-
- Article
- Export citation
Democracy of quasi-greedy bases in $\boldsymbol p$
 -Banach spaces with applications to the efficiency of the Thresholding Greedy Algorithm in the Hardy spaces $\boldsymbol {H_{p}({\mathbb {D}}^{d})}$
-Banach spaces with applications to the efficiency of the Thresholding Greedy Algorithm in the Hardy spaces $\boldsymbol {H_{p}({\mathbb {D}}^{d})}$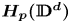
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 24 May 2023, pp. 906-928
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
MIN-PHASE-ISOMETRIES IN STRICTLY CONVEX NORMED SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 22 March 2023, pp. 152-160
- Print publication:
- February 2024
-
- Article
- Export citation
Horseshoes and Lyapunov exponents for Banach cocycles over non-uniformly hyperbolic systems
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 2 / February 2024
- Published online by Cambridge University Press:
- 27 February 2023, pp. 674-704
- Print publication:
- February 2024
-
- Article
- Export citation
New characterizations of the unit vector basis of
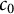 $c_0$ or
$c_0$ or 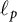 $ \ell _{p}$
$ \ell _{p}$
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 21 February 2023, pp. 1073-1083
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
CONTRACTIVE SEMIGROUPS IN TOPOLOGICAL VECTOR SPACES, ON THE 100TH ANNIVERSARY OF STEFAN BANACH’S CONTRACTION PRINCIPLE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 2 / October 2023
- Published online by Cambridge University Press:
- 11 January 2023, pp. 331-338
- Print publication:
- October 2023
-
- Article
- Export citation
BANACH SPACES IN WHICH LARGE SUBSETS OF SPHERES CONCENTRATE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 2 / March 2024
- Published online by Cambridge University Press:
- 27 December 2022, pp. 737-752
- Print publication:
- March 2024
-
- Article
- Export citation
The complete separation of the two finer asymptotic
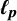 $\boldsymbol {\ell _{p}}$ structures for
$\boldsymbol {\ell _{p}}$ structures for 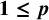 $ \boldsymbol {1\le p}$<
$ \boldsymbol {1\le p}$<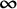 $ \boldsymbol {\infty }$
$ \boldsymbol {\infty }$
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 19 December 2022, e114
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
New parameters and Lebesgue-type estimates in greedy approximation
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 16 December 2022, e113
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Magnitude and Holmes–Thompson intrinsic volumes of convex bodies
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 15 December 2022, pp. 854-867
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The space
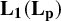 $\mathbf {L_1(L_p)}$ is primary for 1 < p < ∞
$\mathbf {L_1(L_p)}$ is primary for 1 < p < ∞
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 30 May 2022, e32
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Polish spaces of Banach spaces
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 13 May 2022, e26
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Compact and weakly compact Lipschitz operators
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 11 May 2022, pp. 1002-1020
- Print publication:
- June 2023
-
- Article
- Export citation
Spectrality of a class of Moran measures on
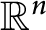 $\mathbb {R}^{n}$ with consecutive digit sets
$\mathbb {R}^{n}$ with consecutive digit sets
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 13 April 2022, pp. 269-285
- Print publication:
- March 2023
-
- Article
- Export citation
Fourier coefficients of functions in power-weighted L2-spaces and conditionality constants of bases in Banach spaces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 30 March 2022, pp. 784-810
- Print publication:
- June 2023
-
- Article
- Export citation
Hausdorff dimension of the set of almost convergent sequences
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 06 January 2022, pp. 691-697
-
- Article
- Export citation
RETRACTED - Compact reduction in Lipschitz-free spaces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 6 / December 2021
- Published online by Cambridge University Press:
- 08 December 2021, pp. 1683-1699
- Print publication:
- December 2021
-
- Article
- Export citation
Interpolation between noncommutative martingale Hardy and BMO spaces: the case
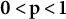 $\textbf {0<p<1}$
$\textbf {0<p<1}$
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 6 / December 2022
- Published online by Cambridge University Press:
- 25 August 2021, pp. 1700-1744
- Print publication:
- December 2022
-
- Article
- Export citation
A new complemented subspace for the Lorentz sequence spaces, with an application to its lattice of closed ideals
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 02 August 2021, pp. 759-769
- Print publication:
- September 2022
-
- Article
- Export citation