Refine listing
Actions for selected content:
291 results in 46Bxx
IMPROVED INEQUALITIES FOR THE NUMERICAL RADIUS: WHEN INVERSE COMMUTES WITH THE NORM
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 2 / April 2018
- Published online by Cambridge University Press:
- 02 February 2018, pp. 293-296
- Print publication:
- April 2018
-
- Article
-
- You have access
- Export citation
A CODING OF BUNDLE GRAPHS AND THEIR EMBEDDINGS INTO BANACH SPACES
- Part of
-
- Journal:
- Mathematika / Volume 64 / Issue 3 / 2018
- Published online by Cambridge University Press:
- 06 August 2018, pp. 847-874
- Print publication:
- 2018
-
- Article
- Export citation
Octahedrality in Lipschitz-free Banach spaces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 3 / June 2018
- Published online by Cambridge University Press:
- 28 December 2017, pp. 447-460
- Print publication:
- June 2018
-
- Article
- Export citation
WIGNER’S THEOREM IN
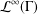 ${\mathcal{L}}^{\infty }(\unicode[STIX]{x1D6E4})$ -TYPE SPACES
${\mathcal{L}}^{\infty }(\unicode[STIX]{x1D6E4})$ -TYPE SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 2 / April 2018
- Published online by Cambridge University Press:
- 04 December 2017, pp. 279-284
- Print publication:
- April 2018
-
- Article
-
- You have access
- Export citation
HILBERT C*-BIMODULES OF FINITE INDEX AND APPROXIMATION PROPERTIES OF C*-ALGEBRAS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 60 / Issue 2 / May 2018
- Published online by Cambridge University Press:
- 17 October 2017, pp. 321-331
- Print publication:
- May 2018
-
- Article
-
- You have access
- Export citation
THE BOUNDED APPROXIMATION PROPERTY FOR THE WEIGHTED SPACES OF HOLOMORPHIC MAPPINGS ON BANACH SPACES
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 60 / Issue 2 / May 2018
- Published online by Cambridge University Press:
- 07 September 2017, pp. 307-320
- Print publication:
- May 2018
-
- Article
-
- You have access
- Export citation
EQUIVARIANT GEOMETRY OF BANACH SPACES AND TOPOLOGICAL GROUPS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 5 / 2017
- Published online by Cambridge University Press:
- 07 September 2017, e22
-
- Article
-
- You have access
- Open access
- Export citation
FIBONACCI–MANN ITERATION FOR MONOTONE ASYMPTOTICALLY NONEXPANSIVE MAPPINGS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 96 / Issue 2 / October 2017
- Published online by Cambridge University Press:
- 13 March 2017, pp. 307-316
- Print publication:
- October 2017
-
- Article
-
- You have access
- Export citation
COMPATIBLE LOCALLY CONVEX TOPOLOGIES ON NORMED SPACES: CARDINALITY ASPECTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 96 / Issue 1 / August 2017
- Published online by Cambridge University Press:
- 13 March 2017, pp. 139-145
- Print publication:
- August 2017
-
- Article
-
- You have access
- Export citation
Corrigendum and Addendum: Abstract M- and Abstract L-Spaces of Polynomials on Banach Lattices
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 4 / November 2017
- Published online by Cambridge University Press:
- 06 January 2017, pp. 877-879
-
- Article
- Export citation
ARRANGEMENTS OF HOMOTHETS OF A CONVEX BODY
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 2 / 2017
- Published online by Cambridge University Press:
- 09 August 2017, pp. 696-710
- Print publication:
- 2017
-
- Article
- Export citation
ISOMETRIC REPRESENTATION OF LIPSCHITZ-FREE SPACES OVER CONVEX DOMAINS IN FINITE-DIMENSIONAL SPACES
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 2 / 2017
- Published online by Cambridge University Press:
- 04 April 2017, pp. 538-552
- Print publication:
- 2017
-
- Article
- Export citation
BRASCAMP–LIEB INEQUALITY AND QUANTITATIVE VERSIONS OF HELLY’S THEOREM
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 1 / 2017
- Published online by Cambridge University Press:
- 07 December 2016, pp. 272-291
- Print publication:
- 2017
-
- Article
- Export citation
BIRKHOFF ORTHOGONALITY IN CLASSICAL
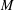 $M$ -IDEALS
$M$ -IDEALS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 103 / Issue 2 / October 2017
- Published online by Cambridge University Press:
- 08 November 2016, pp. 279-288
- Print publication:
- October 2017
-
- Article
-
- You have access
- Export citation
MAPPINGS OF CONSERVATIVE DISTANCES IN
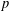 $p$ -NORMED SPACES (
$p$ -NORMED SPACES ( 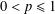 $0<p\leq 1$ )
$0<p\leq 1$ )
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 2 / April 2017
- Published online by Cambridge University Press:
- 02 November 2016, pp. 291-298
- Print publication:
- April 2017
-
- Article
-
- You have access
- Export citation
COMPARING THE GENERALISED ROUNDNESS OF METRIC SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 2 / April 2017
- Published online by Cambridge University Press:
- 02 November 2016, pp. 299-314
- Print publication:
- April 2017
-
- Article
-
- You have access
- Export citation
STRUCTURE TOPOLOGY AND EXTREME OPERATORS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 2 / April 2017
- Published online by Cambridge University Press:
- 19 October 2016, pp. 315-321
- Print publication:
- April 2017
-
- Article
-
- You have access
- Export citation
AN ELEMENTARY PROOF OF JAMES’ CHARACTERISATION OF WEAK COMPACTNESS. II
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 26 September 2016, pp. 133-137
- Print publication:
- February 2017
-
- Article
-
- You have access
- Export citation
SOME INEQUALITIES FOR THE NUMERICAL RADIUS FOR HILBERT SPACE OPERATORS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 3 / December 2016
- Published online by Cambridge University Press:
- 26 September 2016, pp. 489-496
- Print publication:
- December 2016
-
- Article
-
- You have access
- Export citation
Compactness in quasi-Banach function spaces and applications to compact embeddings of Besov-type spaces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 146 / Issue 5 / October 2016
- Published online by Cambridge University Press:
- 23 June 2016, pp. 905-927
- Print publication:
- October 2016
-
- Article
- Export citation
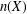
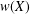
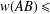
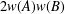
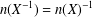
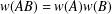
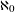
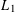
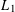
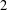
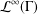
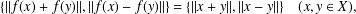
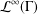
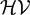
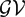
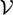
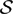
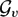
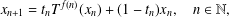
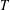
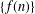
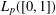
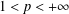

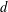
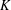
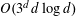
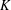
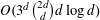
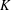
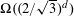
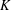
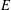
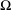
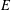
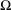
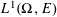
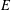
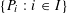
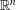
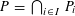
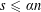
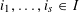
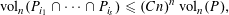
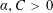
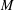
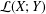
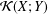
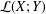
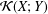
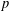
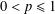
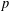
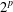
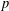

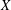
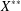

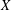
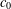
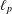
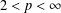
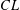
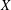
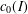
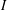
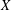
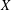
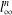
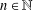
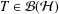
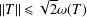
 , into Lorentz-type spaces.
, into Lorentz-type spaces.