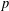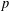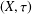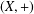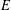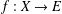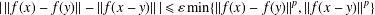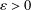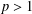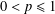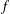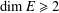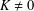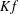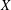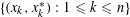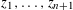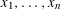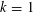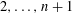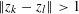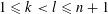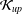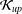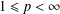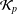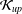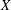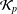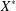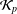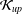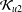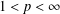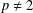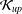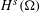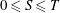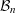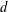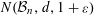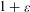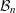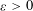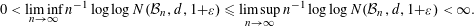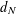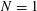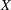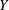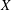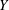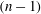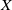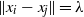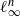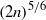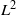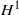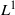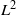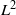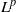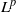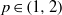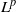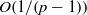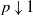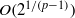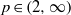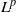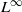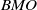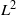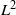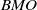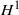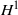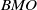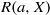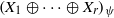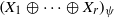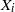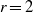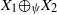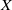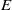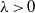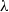Refine listing
Actions for selected content:
291 results in 46Bxx
SEPARATION OF CONVEX SETS IN EXTENDED NORMED SPACES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 99 / Issue 2 / October 2015
- Published online by Cambridge University Press:
- 26 February 2015, pp. 145-165
- Print publication:
- October 2015
-
- Article
-
- You have access
- Export citation
FRAGMENTABILITY BY THE DISCRETE METRIC
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 91 / Issue 2 / April 2015
- Published online by Cambridge University Press:
- 05 January 2015, pp. 303-310
- Print publication:
- April 2015
-
- Article
-
- You have access
- Export citation
ON HYPERSTABILITY OF ADDITIVE MAPPINGS ONTO BANACH SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 91 / Issue 2 / April 2015
- Published online by Cambridge University Press:
- 30 December 2014, pp. 278-285
- Print publication:
- April 2015
-
- Article
-
- You have access
- Export citation
ON THE EXISTENCE OF 1-SEPARATED SEQUENCES ON THE UNIT BALL OF A FINITE-DIMENSIONAL BANACH SPACE
- Part of
-
- Journal:
- Mathematika / Volume 61 / Issue 3 / September 2015
- Published online by Cambridge University Press:
- 05 December 2014, pp. 547-558
- Print publication:
- September 2015
-
- Article
- Export citation
Statistics for Poisson Models of Overlapping Spheres
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 46 / Issue 4 / December 2014
- Published online by Cambridge University Press:
- 22 February 2016, pp. 937-962
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
THE
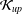 ${\mathcal{K}}_{\mathit{up}}$ -APPROXIMATION PROPERTY AND ITS DUALITY
${\mathcal{K}}_{\mathit{up}}$ -APPROXIMATION PROPERTY AND ITS DUALITY
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 98 / Issue 3 / June 2015
- Published online by Cambridge University Press:
- 20 November 2014, pp. 364-374
- Print publication:
- June 2015
-
- Article
-
- You have access
- Export citation
INTERPOLATION OF HILBERT AND SOBOLEV SPACES: QUANTITATIVE ESTIMATES AND COUNTEREXAMPLES
- Part of
-
- Journal:
- Mathematika / Volume 61 / Issue 2 / May 2015
- Published online by Cambridge University Press:
- 19 November 2014, pp. 414-443
- Print publication:
- May 2015
-
- Article
- Export citation
CHEBYSHEV SETS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 98 / Issue 2 / April 2015
- Published online by Cambridge University Press:
- 11 November 2014, pp. 161-231
- Print publication:
- April 2015
-
- Article
-
- You have access
- Export citation
SOME COMMENTS ON SCALAR DIFFERENTIATION OF VECTOR-VALUED FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 91 / Issue 2 / April 2015
- Published online by Cambridge University Press:
- 11 November 2014, pp. 311-321
- Print publication:
- April 2015
-
- Article
-
- You have access
- Export citation
ON WEAK-FRAGMENTABILITY OF BANACH SPACES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 97 / Issue 2 / October 2014
- Published online by Cambridge University Press:
- 11 June 2014, pp. 251-256
- Print publication:
- October 2014
-
- Article
-
- You have access
- Export citation
DOMINATION BY POSITIVE WEAK
 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}^{*}$ DUNFORD–PETTIS OPERATORS ON BANACH LATTICES
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}^{*}$ DUNFORD–PETTIS OPERATORS ON BANACH LATTICES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 90 / Issue 2 / October 2014
- Published online by Cambridge University Press:
- 05 June 2014, pp. 311-318
- Print publication:
- October 2014
-
- Article
-
- You have access
- Export citation
ON THE METRIC ENTROPY OF THE BANACH–MAZUR COMPACTUM
- Part of
-
- Journal:
- Mathematika / Volume 61 / Issue 1 / January 2015
- Published online by Cambridge University Press:
- 28 May 2014, pp. 179-198
- Print publication:
- January 2015
-
- Article
- Export citation
SPARSE APPROXIMATION AND RECOVERY BY GREEDY ALGORITHMS IN BANACH SPACES
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 2 / 01 July 2014
- Published online by Cambridge University Press:
- 27 May 2014, e12
-
- Article
-
- You have access
- Open access
- Export citation
A FURTHER PROPERTY OF SPHERICAL ISOMETRIES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 90 / Issue 2 / October 2014
- Published online by Cambridge University Press:
- 15 May 2014, pp. 304-310
- Print publication:
- October 2014
-
- Article
-
- You have access
- Export citation
EQUILATERAL SETS IN UNIFORMLY SMOOTH BANACH SPACES
- Part of
-
- Journal:
- Mathematika / Volume 60 / Issue 1 / January 2014
- Published online by Cambridge University Press:
- 02 January 2014, pp. 219-231
- Print publication:
- January 2014
-
- Article
- Export citation
AN EXAMPLE CONCERNING BOUNDED LINEAR REGULARITY OF SUBSPACES IN HILBERT SPACE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 89 / Issue 2 / April 2014
- Published online by Cambridge University Press:
- 12 September 2013, pp. 217-226
- Print publication:
- April 2014
-
- Article
-
- You have access
- Export citation
RESTRICTED INVERTIBILITY AND THE BANACH–MAZUR DISTANCE TO THE CUBE
- Part of
-
- Journal:
- Mathematika / Volume 60 / Issue 1 / January 2014
- Published online by Cambridge University Press:
- 02 September 2013, pp. 201-218
- Print publication:
- January 2014
-
- Article
- Export citation
EXPLICIT INTERPOLATION BOUNDS BETWEEN HARDY SPACE AND
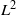 ${L}^{2} $
${L}^{2} $
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 95 / Issue 2 / October 2013
- Published online by Cambridge University Press:
- 18 July 2013, pp. 158-168
- Print publication:
- October 2013
-
- Article
-
- You have access
- Export citation
THE FIXED POINT PROPERTY IN DIRECT SUMS AND MODULUS
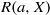 $R(a, X)$
$R(a, X)$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 89 / Issue 1 / February 2014
- Published online by Cambridge University Press:
- 28 June 2013, pp. 79-91
- Print publication:
- February 2014
-
- Article
-
- You have access
- Export citation
INTERSECTIONS OF BALLS AND SETS OF CONSTANT WIDTH IN FINITE-DIMENSIONAL NORMED SPACES
- Part of
-
- Journal:
- Mathematika / Volume 59 / Issue 2 / July 2013
- Published online by Cambridge University Press:
- 28 March 2013, pp. 477-492
- Print publication:
- July 2013
-
- Article
- Export citation