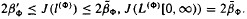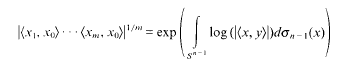Refine listing
Actions for selected content:
291 results in 46Bxx
Ideals of compact operators
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 77 / Issue 1 / August 2004
- Published online by Cambridge University Press:
- 09 April 2009, pp. 91-110
- Print publication:
- August 2004
-
- Article
-
- You have access
- Export citation
Types over c(k) spaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 77 / Issue 1 / August 2004
- Published online by Cambridge University Press:
- 09 April 2009, pp. 17-28
- Print publication:
- August 2004
-
- Article
-
- You have access
- Export citation
Nuclear and integral polynomials
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 76 / Issue 2 / April 2004
- Published online by Cambridge University Press:
- 09 April 2009, pp. 269-280
- Print publication:
- April 2004
-
- Article
-
- You have access
- Export citation
Boundedness of vector-valued martingale transforms on extreme points and applciations
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 76 / Issue 2 / April 2004
- Published online by Cambridge University Press:
- 09 April 2009, pp. 207-222
- Print publication:
- April 2004
-
- Article
-
- You have access
- Export citation
Composition operators in Orlicz spaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 76 / Issue 2 / April 2004
- Published online by Cambridge University Press:
- 09 April 2009, pp. 189-206
- Print publication:
- April 2004
-
- Article
-
- You have access
- Export citation
On Ψ direct sums of Banach spaces and convexity
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 75 / Issue 3 / December 2003
- Published online by Cambridge University Press:
- 09 April 2009, pp. 413-422
- Print publication:
- December 2003
-
- Article
-
- You have access
- Export citation
Computation of nonsquare constants of Orlicz spaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 75 / Issue 2 / October 2003
- Published online by Cambridge University Press:
- 09 April 2009, pp. 153-162
- Print publication:
- October 2003
-
- Article
-
- You have access
- Export citation
Bilinear integration with positive vector measures
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 75 / Issue 2 / October 2003
- Published online by Cambridge University Press:
- 09 April 2009, pp. 279-294
- Print publication:
- October 2003
-
- Article
-
- You have access
- Export citation
Extreme Point Methods and Banach-Stone Theorems
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 75 / Issue 1 / August 2003
- Published online by Cambridge University Press:
- 09 April 2009, pp. 125-143
- Print publication:
- August 2003
-
- Article
-
- You have access
- Export citation
On the geometry of Lp (μ) with applications to infinite variance processes
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 74 / Issue 1 / February 2003
- Published online by Cambridge University Press:
- 09 April 2009, pp. 35-42
- Print publication:
- February 2003
-
- Article
-
- You have access
- Export citation
The Schur and (weak) Dunford-Pettis properties in Banach lattices
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 73 / Issue 2 / October 2002
- Published online by Cambridge University Press:
- 09 April 2009, pp. 251-278
- Print publication:
- October 2002
-
- Article
-
- You have access
- Export citation
Lipschitz quotient mappings with good ratio of constants
- Part of
-
- Journal:
- Mathematika / Volume 49 / Issue 1-2 / June 2002
- Published online by Cambridge University Press:
- 26 February 2010, pp. 159-165
- Print publication:
- June 2002
-
- Article
- Export citation
Generalized contact distributions of inhomogeneous Boolean models
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 34 / Issue 1 / March 2002
- Published online by Cambridge University Press:
- 19 February 2016, pp. 21-47
- Print publication:
- March 2002
-
- Article
- Export citation
A phase transition phenomenon between the isometric and isomorphic extension problems for Hölder functions between Lp spaces
- Part of
-
- Journal:
- Mathematika / Volume 48 / Issue 1-2 / December 2001
- Published online by Cambridge University Press:
- 26 February 2010, pp. 253-271
- Print publication:
- December 2001
-
- Article
- Export citation
A note on porosity and the Mazur intersection property
- Part of
-
- Journal:
- Mathematika / Volume 47 / Issue 1-2 / December 2000
- Published online by Cambridge University Press:
- 26 February 2010, pp. 267-272
- Print publication:
- December 2000
-
- Article
- Export citation
Lower bounds for multilinear forms defined on Hilbert Spaces
- Part of
-
- Journal:
- Mathematika / Volume 46 / Issue 2 / December 1999
- Published online by Cambridge University Press:
- 26 February 2010, pp. 315-322
- Print publication:
- December 1999
-
- Article
- Export citation
Continuous functions on products of compact Hausdorff spaces
- Part of
-
- Journal:
- Mathematika / Volume 46 / Issue 2 / December 1999
- Published online by Cambridge University Press:
- 26 February 2010, pp. 323-330
- Print publication:
- December 1999
-
- Article
- Export citation
Locally uniformly rotund norms
- Part of
-
- Journal:
- Mathematika / Volume 46 / Issue 2 / December 1999
- Published online by Cambridge University Press:
- 26 February 2010, pp. 343-358
- Print publication:
- December 1999
-
- Article
- Export citation
An algebraic approach to Wigner's unitary-antiunitary theorem
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 65 / Issue 3 / December 1998
- Published online by Cambridge University Press:
- 09 April 2009, pp. 354-369
- Print publication:
- December 1998
-
- Article
-
- You have access
- Export citation
Integral means on radially weighted spaces of analytic functions
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 65 / Issue 1 / August 1998
- Published online by Cambridge University Press:
- 09 April 2009, pp. 68-83
- Print publication:
- August 1998
-
- Article
-
- You have access
- Export citation
 (
( into
into 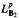 for some
for some 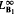 into
into 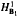 into
into 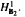 . Applications to
. Applications to 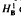 defined in the case of a general filtration has nice dense sets and nice atomic decompositions if and only if Β has the Radon-Nikodým property.
defined in the case of a general filtration has nice dense sets and nice atomic decompositions if and only if Β has the Radon-Nikodým property.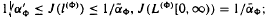 (ii) if φ (
(ii) if φ (