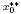Refine listing
Actions for selected content:
291 results in 46Bxx
ISOMETRIES BETWEEN UNIT SPHERES OF THE
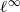 ${\ell }^{\infty } $-SUM OF STRICTLY CONVEX NORMED SPACES
${\ell }^{\infty } $-SUM OF STRICTLY CONVEX NORMED SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 88 / Issue 3 / December 2013
- Published online by Cambridge University Press:
- 28 March 2013, pp. 369-375
- Print publication:
- December 2013
-
- Article
-
- You have access
- Export citation
ON A WEAKLY UNIFORMLY ROTUND DUAL OF A BANACH SPACE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 92 / Issue 1 / August 2015
- Published online by Cambridge University Press:
- 01 August 2012, e1
- Print publication:
- August 2015
-
- Article
-
- You have access
- Export citation
REPRESENTATION THEOREMS FOR INDEFINITE QUADRATIC FORMS REVISITED
- Part of
-
- Journal:
- Mathematika / Volume 59 / Issue 1 / January 2013
- Published online by Cambridge University Press:
- 12 June 2012, pp. 169-189
- Print publication:
- January 2013
-
- Article
- Export citation
A lower bound on the waist of unit spheres of uniformly convex normed spaces
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 4 / July 2012
- Published online by Cambridge University Press:
- 15 May 2012, pp. 1238-1264
- Print publication:
- July 2012
-
- Article
-
- You have access
- Export citation
Spectrality of self-affine measures on the three-dimensional Sierpinski gasket
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 55 / Issue 2 / June 2012
- Published online by Cambridge University Press:
- 20 April 2012, pp. 477-496
-
- Article
-
- You have access
- Export citation
A quantitative version of James's Compactness Theorem
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 55 / Issue 2 / June 2012
- Published online by Cambridge University Press:
- 23 February 2012, pp. 369-386
-
- Article
-
- You have access
- Export citation
ULTRAPOWERS OF ℓ1-MUNN ALGEBRAS AND THEIR APPLICATION TO SEMIGROUP ALGEBRAS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 86 / Issue 3 / December 2012
- Published online by Cambridge University Press:
- 25 January 2012, pp. 424-429
- Print publication:
- December 2012
-
- Article
-
- You have access
- Export citation
Poincaré inequalities, embeddings, and wild groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 5 / September 2011
- Published online by Cambridge University Press:
- 24 August 2011, pp. 1546-1572
- Print publication:
- September 2011
-
- Article
-
- You have access
- Export citation
AN ELEMENTARY PROOF OF JAMES’ CHARACTERIZATION OF WEAK COMPACTNESS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 84 / Issue 1 / August 2011
- Published online by Cambridge University Press:
- 03 June 2011, pp. 98-102
- Print publication:
- August 2011
-
- Article
-
- You have access
- Export citation
STATES ON THE CUNTZ ALGEBRAS AND p-ADIC RANDOM WALKS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 90 / Issue 2 / April 2011
- Published online by Cambridge University Press:
- 19 July 2011, pp. 197-211
- Print publication:
- April 2011
-
- Article
-
- You have access
- Export citation
A CONTINUITY CHARACTERIZATION OF ASPLUND SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 83 / Issue 3 / June 2011
- Published online by Cambridge University Press:
- 07 February 2011, pp. 450-455
- Print publication:
- June 2011
-
- Article
-
- You have access
- Export citation
ON λ-STRICT IDEALS IN BANACH SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 83 / Issue 2 / April 2011
- Published online by Cambridge University Press:
- 27 September 2010, pp. 231-240
- Print publication:
- April 2011
-
- Article
-
- You have access
- Export citation
Corrigendum: amenability of ultrapowers of Banach algebras
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 53 / Issue 3 / October 2010
- Published online by Cambridge University Press:
- 16 August 2010, pp. 633-637
-
- Article
-
- You have access
- Export citation
Transitivity in spaces of vector-valued functions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 53 / Issue 3 / October 2010
- Published online by Cambridge University Press:
- 05 August 2010, pp. 601-608
-
- Article
-
- You have access
- Export citation
Isometries on extremely non-complex Banach spaces
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 10 / Issue 2 / April 2011
- Published online by Cambridge University Press:
- 14 July 2010, pp. 325-348
- Print publication:
- April 2011
-
- Article
- Export citation
ON STRICTLY SINGULAR OPERATORS BETWEEN SEPARABLE BANACH SPACES
- Part of
-
- Journal:
- Mathematika / Volume 56 / Issue 2 / July 2010
- Published online by Cambridge University Press:
- 22 June 2010, pp. 285-304
- Print publication:
- July 2010
-
- Article
- Export citation
TILINGS OF HILBERT SPACES
- Part of
-
- Journal:
- Mathematika / Volume 56 / Issue 2 / July 2010
- Published online by Cambridge University Press:
- 29 April 2010, pp. 217-230
- Print publication:
- July 2010
-
- Article
- Export citation
ASYMPTOTIC PROPERTIES OF KOLMOGOROV WIDTHS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 82 / Issue 1 / August 2010
- Published online by Cambridge University Press:
- 25 March 2010, pp. 10-17
- Print publication:
- August 2010
-
- Article
-
- You have access
- Export citation
NONCOMPLETE MACKEY TOPOLOGIES ON BANACH SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 81 / Issue 3 / June 2010
- Published online by Cambridge University Press:
- 05 March 2010, pp. 409-413
- Print publication:
- June 2010
-
- Article
-
- You have access
- Export citation
Markov Type of Alexandrov Spaces of Non-Negative Curvature Shin-Ichi Ohta
- Part of
-
- Journal:
- Mathematika / Volume 55 / Issue 1-2 / December 2009
- Published online by Cambridge University Press:
- 21 December 2009, pp. 177-189
- Print publication:
- December 2009
-
- Article
- Export citation
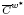 ⊂
⊂