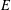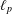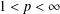Refine listing
Actions for selected content:
291 results in 46Bxx
OPERATOR SYSTEM NUCLEARITY VIA
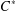 $C^{\ast }$ -ENVELOPES
$C^{\ast }$ -ENVELOPES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 101 / Issue 3 / December 2016
- Published online by Cambridge University Press:
- 11 May 2016, pp. 356-375
- Print publication:
- December 2016
-
- Article
-
- You have access
- Export citation
On the loss of compactness in the vectorial heteroclinic connection problem
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 146 / Issue 3 / June 2016
- Published online by Cambridge University Press:
- 22 March 2016, pp. 595-608
- Print publication:
- June 2016
-
- Article
- Export citation
METRIC
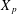 $X_{p}$ INEQUALITIES
$X_{p}$ INEQUALITIES
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 4 / 2016
- Published online by Cambridge University Press:
- 02 February 2016, e3
-
- Article
-
- You have access
- Open access
- Export citation
BUZANO’S INEQUALITY HOLDS FOR ANY PROJECTION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 3 / June 2016
- Published online by Cambridge University Press:
- 20 January 2016, pp. 504-510
- Print publication:
- June 2016
-
- Article
-
- You have access
- Export citation
A LIMITING CASE OF ULTRASYMMETRIC SPACES
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 3 / 2016
- Published online by Cambridge University Press:
- 01 June 2016, pp. 929-948
- Print publication:
- 2016
-
- Article
- Export citation
ON THE STRUCTURE OF SEPARABLE
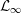 ${\mathcal{L}}_{\infty }$ -SPACES
${\mathcal{L}}_{\infty }$ -SPACES
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 3 / 2016
- Published online by Cambridge University Press:
- 07 March 2016, pp. 685-700
- Print publication:
- 2016
-
- Article
- Export citation
ON ISOMETRIC REPRESENTATION SUBSETS OF BANACH SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 3 / June 2016
- Published online by Cambridge University Press:
- 11 December 2015, pp. 486-496
- Print publication:
- June 2016
-
- Article
-
- You have access
- Export citation
MAZUR–ULAM PROPERTY OF THE SUM OF TWO STRICTLY CONVEX BANACH SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 3 / June 2016
- Published online by Cambridge University Press:
- 11 November 2015, pp. 473-485
- Print publication:
- June 2016
-
- Article
-
- You have access
- Export citation
NEAREST POINTS AND DELTA CONVEX FUNCTIONS IN BANACH SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 2 / April 2016
- Published online by Cambridge University Press:
- 03 September 2015, pp. 283-294
- Print publication:
- April 2016
-
- Article
-
- You have access
- Export citation
CHAINS OF FUNCTIONS IN
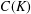 $C(K)$-SPACES
$C(K)$-SPACES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 99 / Issue 3 / December 2015
- Published online by Cambridge University Press:
- 02 September 2015, pp. 350-363
- Print publication:
- December 2015
-
- Article
-
- You have access
- Export citation
SPECTRUM AND COMPACTNESS OF THE CESÀRO OPERATOR ON WEIGHTED
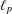 $\ell _{p}$ SPACES
$\ell _{p}$ SPACES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 99 / Issue 3 / December 2015
- Published online by Cambridge University Press:
- 19 August 2015, pp. 287-314
- Print publication:
- December 2015
-
- Article
-
- You have access
- Export citation
GROUP ACTION PRESERVING THE HAAGERUP PROPERTY OF
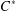 $C^{\ast }$-ALGEBRAS
$C^{\ast }$-ALGEBRAS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 2 / April 2016
- Published online by Cambridge University Press:
- 11 August 2015, pp. 295-300
- Print publication:
- April 2016
-
- Article
-
- You have access
- Export citation
A WEAKLY UNIFORMLY ROTUND DUAL OF A BANACH SPACE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 92 / Issue 3 / December 2015
- Published online by Cambridge University Press:
- 10 August 2015, pp. 457-462
- Print publication:
- December 2015
-
- Article
-
- You have access
- Export citation
STABILITY OF UNCONDITIONAL SCHAUDER DECOMPOSITIONS IN
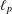 $\ell _{p}$ SPACES
$\ell _{p}$ SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 92 / Issue 3 / December 2015
- Published online by Cambridge University Press:
- 03 August 2015, pp. 444-456
- Print publication:
- December 2015
-
- Article
-
- You have access
- Export citation
FRACTAL BASES FOR BANACH SPACES OF SMOOTH FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 92 / Issue 3 / December 2015
- Published online by Cambridge University Press:
- 30 July 2015, pp. 405-419
- Print publication:
- December 2015
-
- Article
-
- You have access
- Export citation
NON-UNITARISABLE REPRESENTATIONS AND MAXIMAL SYMMETRY
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 16 / Issue 2 / April 2017
- Published online by Cambridge University Press:
- 01 July 2015, pp. 421-445
- Print publication:
- April 2017
-
- Article
- Export citation
Boundedness of integral operators on decreasing functions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 145 / Issue 4 / August 2015
- Published online by Cambridge University Press:
- 30 June 2015, pp. 725-744
- Print publication:
- August 2015
-
- Article
- Export citation
ON A QUESTION OF BOURAS CONCERNING WEAK COMPACTNESS OF ALMOST DUNFORD–PETTIS SETS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 92 / Issue 1 / August 2015
- Published online by Cambridge University Press:
- 02 April 2015, pp. 111-114
- Print publication:
- August 2015
-
- Article
-
- You have access
- Export citation
ON THE ALEKSANDROV–RASSIAS PROBLEM OF DISTANCE PRESERVING MAPPINGS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 91 / Issue 3 / June 2015
- Published online by Cambridge University Press:
- 17 March 2015, pp. 464-470
- Print publication:
- June 2015
-
- Article
-
- You have access
- Export citation
ON QUANTITATIVE SCHUR AND DUNFORD–PETTIS PROPERTIES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 91 / Issue 3 / June 2015
- Published online by Cambridge University Press:
- 26 February 2015, pp. 471-486
- Print publication:
- June 2015
-
- Article
-
- You have access
- Export citation
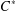
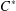
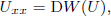
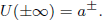
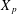
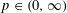
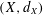
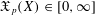
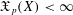
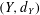
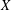
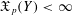
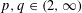
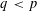
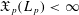
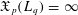
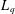
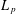
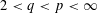
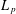
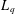
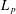
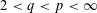
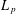
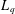
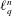
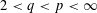
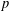
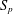
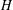
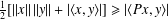
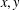
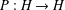

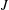

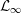
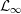
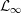
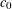
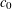
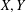
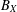
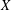
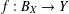
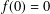
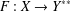
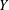
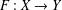
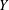
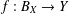
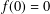
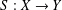
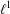
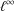
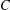
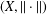
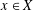
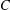
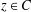
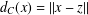

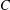
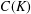
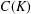
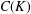
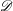
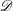
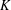
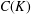
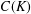
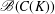
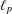
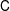
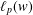
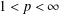
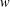
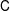
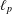

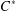
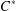
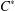
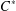
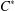
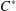
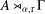
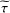
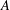

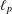
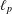
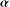
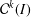
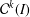
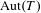
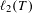

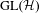
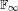
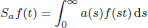
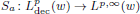 was completely solved, the characterization of the weights
was completely solved, the characterization of the weights 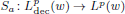 is bounded is still open for the case in which
is bounded is still open for the case in which